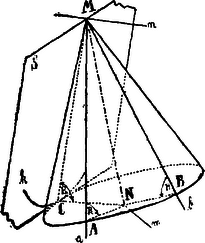
I. Megoldás. Mivel az egyenes körkúpnál minden alkotónak a csúcspont és alapkör közti hossza egyenlő, ezért $M$-ből az $a$ és $b$ egyenesekre egyenlő $d$ távolságot mérünk fel és így az $A$ és $B$ pontokat kapjuk. Hasonlóképpen $M$-ből $S$-en $d$ sugárral kört rajzolunk, hogy az érintési alkotónak az alapkörön lévő $C$ pontját megkaphassuk. Legyen $\left(|AB|S\right)=D$, akkor $\overline{D{C}^2}=\overline{DA}\cdot \overline{DB}$, mert egy kívülfekvő pontból az (alap) körhöz húzott érintő négyzete egyenlő a szelők szeleteinek szorzatával. $\overline{DC}$ a mértani középarányossal megszerkeszthető. $D$-ből $S$-en $\overline{DC}$ sugárral rajzolt kör metszi a $d$ sugarú kört $C$-ben. $A$, $B$, $C$ a keresett kúp alapkörének 3 pontja és $MC$ az érintési alkotó.
A megoldások száma kettő, mert két $C$ pont szerkeszthető. Az $a$ és $b$ alkotókra két irányban felmért $A_1{A}_2$, $B_1{B}_2$ pontok nem adnak új megoldást.