Kezdőlap


Feladat:	1103. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	(A.) , Bartók I. , Haar A.
Füzet:	1905/június, 209 - 210. oldal		PDF \| MathML
Témakör(ök):	Négyszögek geometriája, Párhuzamos szelők tétele, Feladat
Hivatkozás(ok):	Feladatok: 1902/december: 1103. matematika feladat

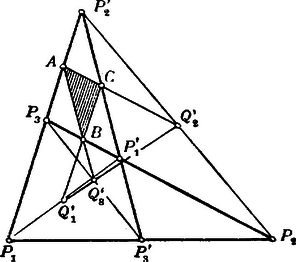
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{\circ}$ . Tételünket először abban a speciális esetben akarjuk bebizonyítani, midőn a $Q_{1}, Q_{2}, Q_{3}$ pontok a $P_{1} P'_{1}, P_{2} P'_{2}, P_{3} P'_{3}$ egyenesek végtelenben fekvő pontjai, tehát $Q_{1}, Q_{2}, Q_{3}$ pontok rendre felezik a $P_{1} P'_{1}, P_{2} P'_{2}, P_{3} P'_{3}$ diagonálisokat. A bizonyítandó tétel tehát ez esetben:
"A teljes négyoldal átlóinak felezéspontjai egy egyenesben vannak."
Bizonyítás. Jelöljék $A, B, C$ a $P'_{2} P_{3}, P_{3} P'_{1}$ , illetőleg a $P'_{1} P'_{2}$ távolságok felezéspontjait, akkor

\begin{matrix} A B ∥ P'_{2} P'_{1} \end{matrix}

\begin{matrix} B C ∥ P_{3} P'_{2} \end{matrix}

(1)

\begin{matrix} C A ∥ P'_{1} P_{3}, \end{matrix}

tehát

A B, B C, C A

felezik a

P_{3} P'_{3}, P_{1} P'_{1}

, illetve a

P_{2} P'_{2}

diagonálisokat is, és így átmennek a

Q'_{3}, Q'_{1}, Q'_{2}

pontokon.
Már most a

P'_{1} P'_{2} P_{3}

háromszögnek a

P_{1} P'_{3} P_{2}

transversálisa, tehát a Menelaos-féle tétel értelmében:

\begin{matrix} \frac{P'_{1} P'_{3}}{P'_{2} P'_{3}} \cdot \frac{P'_{2} P_{1}}{P_{3} P_{1}} \cdot \frac{P_{3} P_{2}}{P'_{1} P_{3}} = 1. \end{matrix}

(2)

Ámde

(1)

következtében:

\begin{matrix} \frac{P'_{1} P'_{3}}{P'_{2} P'_{3}} = \frac{B Q'_{3}}{A Q'_{3}} \end{matrix}

\begin{matrix} \frac{P'_{2} P_{1}}{P_{3} P_{1}} = \frac{C Q'_{1}}{B Q'_{1}} \end{matrix}

\begin{matrix} \frac{P_{3} P_{2}}{P'_{1} P_{3}} = \frac{A Q'_{2}}{C Q'_{2}} \end{matrix}

amit

(1)

-be téve nyerjük:

\begin{matrix} \frac{B Q'_{3}}{A Q'_{3}} \cdot \frac{C Q'_{1}}{B Q'_{1}} \cdot \frac{A Q'_{2}}{C Q'_{2}} = 1, \end{matrix}

(3)

ami Menelaos tétele értelmében azt mondja, hogy az

A B C

háromszög oldalain fekvő

Q_{1}, Q_{2}, Q_{3}

pontok egyazon egyenesen vannak.

2^{\circ}

. Az általános esetben felveszünk a térben egy

S

pontot és az egész alakzatot egy az

(S_{p})

síkkal párhuzamos síkra vetítjük. E projekcióban a

p

-nek megfelelő egyenes végtelenbe jut, tehát az előző tétel értelmében a

Q'_{1}, Q'_{2} Q'_{3}

pontok vetületei egyazon egyenesben vannak, amiből azonban máris következik, hogy a

Q'_{1}, Q'_{2} Q'_{3}

maguk is egy egyenesen fekszenek.

(A.)