Kezdőlap


Feladat:	1053. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Ádámffy E. , Bánó L. , Dömény I. , Erdős V. , Friedländer H. , Füstös P. , Földes R. , Gunszt B. , Haar A. , Harsányi Z. , Kertész G. , Kovács Gyula , Kürti Imre , Messer P. , Paunz Arthur , Riesz Marcell , Rosenthal M. , Schwarz Gy. , Schöffer I. , Sonnenfeld J. , Strobl J. , Söpkéz Gy. , Tóth B.
Füzet:	1902/december, 118 - 120. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Húrsokszögek, Szabályos sokszögek geometriája, Terület, felszín, Háromszögek egybevágósága, Síkidomok átdarabolása, Feladat
Hivatkozás(ok):	Feladatok: 1902/szeptember: 1053. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A tizenkétszög szerkesztéséből következik, hogy az $O A B Δ B$ csúcsa az $O D$ sugarat merőlegesen felező egyenesbe esik.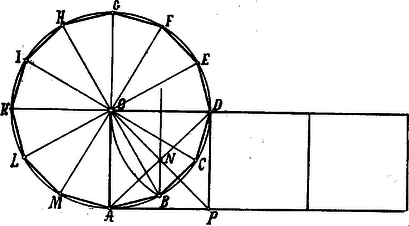

O A P D

négyzet átlóinak

N

metszési pontja ugyancsak eme egyenesbe esik. Minthogy az

O A B

és

O A N

háromszögek alapja közös,

B

illetőleg

N

csúcsuk pedig az alappal párhuzamos egyenesen van, azért e két háromszög egyenlő területű. De a

3 r

alapú és

r

magasságú téglalap területe

\begin{matrix} 3 \cdot O A P D = 12 \cdot O A N = 12 \cdot O A B \end{matrix}

továbbá a tizenkétszög területe szintén

\begin{matrix} 12 \cdot O A B \end{matrix}

s így a tizenkétszög területe csakugyan egyenlő oly téglalap területével, melynek alapja

3 r

, magassága

r

(Paunz Arthur, Pécs.)

II. megoldás. A tizenkétszöget ismét szétbontjuk

12

egybevágó, egyenlőszárú háromszögre.

Ábránk mutatja, hogy a sugarak fölé rajzolt

3

négyzet magában foglalja a sokszög

9

háromszögét. Ennélfogva csak azt kell kimutatnunk, hogy a négyzetekből még megmaradó

3

ötszög területe egyenlő a tizenkészög

3

háromszögének területével, vagyis, hogy egy ötszög területe egyenlő egy háromszög területével.
Könnyen kimutatható, hogy

\begin{matrix} D O C Δ ≅ P F D Δ és F E D Δ ≅ P D C Δ, \end{matrix}

\begin{matrix} P F D = P F E D + F E D = P F E D + P D C = P F E D C . \end{matrix}

S így az ötszög területe csakugyan egyenlő a

D O C

háromszög területével.

(Kovács Gyula, Budapest.)

III. megoldás. A tizenkétszöget felbontjuk hat egybevágó négyszögre. Ilyen pl.

O A B C

Bebizonyítjuk, hogy két ily négyszög területének összege egyenlő oly négyzet területével, melynek mindegyik oldala

r

. Legyen ilyen négyzet

H I K L

H I

fölé szabályos háromszöget rajzolunk; ekkor

\begin{matrix} O A C Δ ≅ H M I Δ . \end{matrix}

Továbbá könnyen kimutatható, hogy: Könnyen kimutatható, hogy

\begin{matrix} C O D Δ ≅ L H M Δ, \end{matrix}

\begin{matrix} D O E Δ ≅ K I M Δ, \end{matrix}

\begin{matrix} A B C Δ ≅ K M L Δ \end{matrix}

s így csakugyan

\begin{matrix} O A B C D E = H I K L . \end{matrix}

(Riesz Marczel, Győr.)

IV. megoldás. A feladatnak egy egyszerű megoldását mutatja a következő ábra.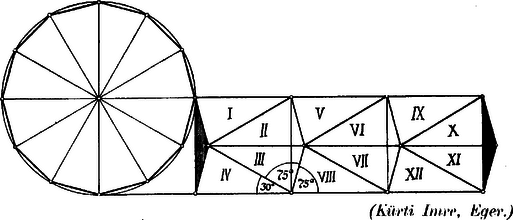

A feladatot még megoldották: Ádámffy E., Bánó L., Dömény I., Erdős V., Földes R., Friedländer H., Füstös P., Gunszt B., Haar A., Harsányi Z., Kertész G., Messer P., Rosenthal M., Schöffer I., Schwarz Gy., Sonnenfeld J., Söpkéz Gy., Strobl J., Tóth B.