Kezdőlap


Feladat:	949. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bartók I. , Deutsch I. , Kőnig Dénes , Pivnyik I.
Füzet:	1902/április, 216 - 218. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Egyéb sokszögek hasonlósága, Paralelogrammák, Feladat
Hivatkozás(ok):	Feladatok: 1901/szeptember: 949. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Első segédtétel. Valamely szög szárain felvesszük a $P P_{1} = a$ és $Q Q_{1} = b$ állandó hosszúságú vonaldarabokat. Kimutatjuk, hogy $P Q$ és $P_{1} Q_{1}$ egyenesek középpontjait összekötő egyenes iránya nem változik, bárhol vesszük is fel az állandó $a$ és $b$ távolságokat. (1. ábra.)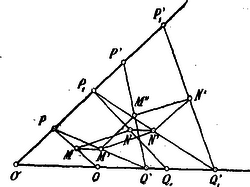

Toljuk ugyanis

Q Q_{1}

-et a

Q' Q'_{1}

helyzetbe és legyenek a

P Q

P Q'

P_{1} Q_{1}

P_{1} Q'_{1}

távolságok középpontjai rendre:

M, M', N, N'

. Minthogy

M M'

és

N N'

P Q Q'

, illetőleg a

P_{1} Q_{1} Q'_{1}

háromszögek két-két oldalfelező pontjának összekötő egyenesei, azért:

\begin{matrix} M M' = \frac{1}{2} Q Q', N N' = \frac{1}{2} Q_{1} Q_{1}' \end{matrix}

és

\begin{matrix} M M' ∥ Q Q' N N' ∥ Q_{1} Q_{1}' . \end{matrix}

Ámde

Q Q'

és

Q_{1} Q_{1}'

egy egyenesbe esnek és

Q Q_{1} = Q' Q_{1}'

, tehát

\begin{matrix} M M' = N N' \end{matrix}

és

\begin{matrix} M M' ∥ N N' . \end{matrix}

M M' N' N

tehát parallelogramma és így az

M N

tényleg párhuzamos

M' N'

-nel. Most ismét

P P_{1}

-et tolhatjuk a tetszőleges

P' P_{1}'

helyzetbe. Ha

P' Q'

középpontját

M''

-mel,

P_{1}' Q_{1}'

középpontját

N''

-nel jelölöm, akkor éppúgy, mint előbb

\begin{matrix} M'' N'' ∥ M' N' tehát ∥ M N \end{matrix}

miáltal tételünk beigazolást is nyert.
Az állandó

M N

irányt legegyszerűbben úgy nyerhetjük, ha

P

-t és

Q

-t is a szög

O

csúcspontjában vesszük fel és ezt összekötjük

P' Q'

-nak

N

középpontjával. Ezen összekötő egyenes felezi minden

P' Q'

-val párhuzamos egyenesnek a szög szárai közt lévő részét és mivel minden ilyen parallel egyenes

O

-tól kezdve

O P' : O Q'

arányú szeleteket vág le a szárakból és viszont, ha két ily szelet viszonya

O P' : O Q'

, akkor a végpontjait összekötő egyenes párhuzamos

P' Q'

-val, azért érvényes a következő tétel is:
Második segédtétel. Az MN irány akkor is állandó marad, ha a

P P_{1}

és

Q Q_{1}

vonaldaraboknak csak a viszonyuk állandó.
Ezek után áttérünk a kitűzött tétel bizonyítására: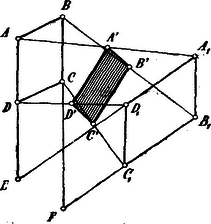

1^{\circ} . (2.

ábra.) Legyen

A D

és

A_{1} D_{1}

metszése

E

-ben;

B C

és

B_{1} C_{1}

metszéspontia pedig

F

-ben, akkor

\begin{matrix} A E A_{1} ∢ = B F B_{1} ∢ \end{matrix}

(száraik párhuzamosak) és

\begin{matrix} A D = B C és A_{1} D_{1} = B_{1} C_{1}, \end{matrix}

tehát az első segédtétel értelmében

A' D'

A_{1} D_{1} E

-vel épp akkora szöget zár be, mint

B' C'

B_{1} C_{1} F

egyenessel. Ámde:

\begin{matrix} A_{1} D_{1} ∥ B_{1} C_{1} \end{matrix}

és így

\begin{matrix} A' D' ∥ B' C' . \end{matrix}

Hasonlóképpen

\begin{matrix} A' B' ∥ D' C', \end{matrix}

tehát

A' B' C' D'

csakugyan parallelogramma.

2^{\circ}

. Legyenek most az adott parallelogrammák hasonlók. (3. ábra.)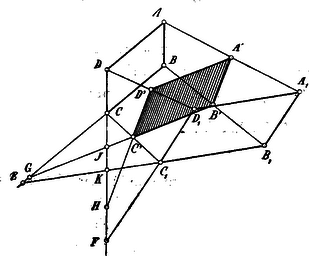

Ki fogjuk mutatni, hogy

\begin{matrix} B' C' D' △ \sim B C D △ \end{matrix}

és

\begin{matrix} A' B' D' △ \sim A B D △ \end{matrix}

mi által tételünk második fele is beigazolást nyer. Nevezzük e végből

B C

és

B_{1} C_{1}

metszéspontját

E

-nek,

D C

és

D_{1} C_{1}

metszését

F

-nek és a

D C

meg

B_{1} C_{1}

metszéspontját

K

-nak; akkor minthogy

\begin{matrix} D C B ∢ = D_{1} C_{1} B_{1} ∢ \end{matrix}

azért

\begin{matrix} E C K ∢ = K C_{1} F ∢ . \end{matrix}

Továbbá

\begin{matrix} C K E ∢ = C_{1} K F ∢ \end{matrix}

és így

\begin{matrix} C K E △ \sim C_{1} K F △, \end{matrix}

tehát

\begin{matrix} K E C ∢ = K F C_{1} ∢ . \end{matrix}

Mivel

A B C D \sim A_{1} B_{1} C_{1} D_{1}

, azért a

K E C

szárain lévő

B C

és

B_{1} C_{1}

szeletek aránya egyenlő a

K F C_{1} ∢

szárain lévő

D C

és

D_{1} C_{1}

szeletek arányával. Második segédtételünk értelmében tehát:

\begin{matrix} C G C' ∢ \sim C H C' ∢, \end{matrix}

hol

G

B C

és

B' C'

egyenesek,

H

pedig a

D C

és

D' C'

egyenesek metszése. Ha

D C

B' C'

-t

I

-ben metszi, akkor tehát:

\begin{matrix} C G I △ \sim C' H I △, \end{matrix}

miért is

\begin{matrix} G C I ∢ = H C' I ∢ \end{matrix}

és csúcsszögeik:

\begin{matrix} D C B ∢ = D' C' B' ∢ . \end{matrix}

Hasonlóképpen kimutatható, hogy a

B' C' D' △

többi szögei s az

A' B' D' △

szögei is a

B C D △

többi szögeivel, illetőleg az

A B D △

szögeivel egyenlők, tehát valóban:

\begin{matrix} A B C D \sim A' B' C,' D' \sim A_{1} B_{1} C_{1} D_{1} . \end{matrix}

(König Dénes. Budapest.

A feladatot még megoldották: Bartók I., Deutsch I., Pivnyik I.