Feladat:	919. matematika feladat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Bartók I. ,  Bayer B. ,  Dömény I. ,  Hirschfeld Gy. ,  Kertész F. ,  Kertész G. ,  König D. ,  Lázár L. ,  Pilczer P. ,  Pivnyik I. ,  Póka Gy. ,  Riesz K. ,  Riesz M. ,  Schmidl I. ,  Simon S. ,  Sümegi Gy. ,  Szmodics Hidegárd ,  Tóbiás J. L.
Füzet:	1902/december, 108 - 109. oldal		PDF  |  MathML
Témakör(ök):	Egyéb feladványok, Feladat
Hivatkozás(ok):	Feladatok: 1901/február: 919. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.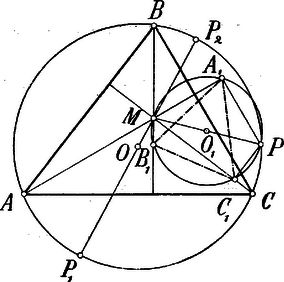   $1^{\circ }$. Kössük össze $P$-t a magassági ponttal, $M$-mel, akkor: $\begin{array}{c}{\displaystyle M{A}_{1}P\sphericalangle =M{B}_{1}P\sphericalangle =M{C}_{1}P\sphericalangle ={90}^{\circ }\mathrm{,}}\end{array}$ tehát $A_1\mathrm{,}{B}_1\mathrm{,}{C}_1\mathrm{,}M\mathrm{,}P$ pontok kerületén feküsznek, miért is: $\begin{array}{c}{\displaystyle A_1{B}_1{C}_1\sphericalangle ={180}^{\circ }-A_{1}P{C}_1\sphericalangle \mathrm{,}}\end{array}$ $\begin{array}{c}{\displaystyle B_1{C}_1{A}_1\sphericalangle =BP{A}_1\sphericalangle }\end{array}$ és $\begin{array}{c}{\displaystyle C_1{A}_1{B}_1\sphericalangle =C_{1}P{B}_1\sphericalangle \mathrm{,}}\end{array}$ mint ugyanazon íven nyugvó kerületi szögek. Ámde: $\begin{array}{c}{\displaystyle A_{1}P{C}_1\sphericalangle ={180}^{\circ }-ABC\sphericalangle ={180}^{\circ }-\beta \sphericalangle }\end{array}$ $\begin{array}{c}{\displaystyle B_{1}P{A}_1\sphericalangle =BCA\sphericalangle =\gamma \sphericalangle }\end{array}$ $\begin{array}{c}{\displaystyle C_{1}P{B}_1\sphericalangle =CAB\sphericalangle =\alpha \sphericalangle \mathrm{,}}\end{array}$ minthogy száraik a megfelelő magasságvonalakra merőlegesek. Igaz tehát,hogy: vagyis $\begin{array}{c}{\displaystyle A_1{B}_1{C}_1\Delta \sim ABC\Delta \mathrm{.}}\end{array}$ $2^{\circ }$. Az $A_1{B}_1{C}_1$ háromszög területe, ha $r_1$ a körülírt kör sugara: $A_1{B}_1{C}_1=\frac{A_1{B}_1\cdot B_1{C}_1\cdot C_1{A}_1}{4r_1}=2r_1^2\text{sin}\alpha \text{sin}\beta \text{sin}\gamma =\frac{{\overline{MP}}^2}{2}\text{sin}\alpha \text{sin}\beta \text{sin}\gamma$, mert $\begin{array}{c}{\displaystyle A_1{B}_1=2r_1\text{sin}\alpha \text{é. í. t.}}\end{array}$ Látható, hogy az $A_1{B}_1{C}_1$ háromszög területe csak $MP$-től függ. $MP$ pedig akkor éri el minimumát, illetőleg maximumát, ha az keresztül megy az $ABC$ kör $O$ középpontján. Ha tehát $OM$ az $ABC$ kört $P_1$ és $P_2$-ben metszi és az elsőhöz az $A_1{B}_1{C}_1$, a másodikhoz pedig az $A_2{B}_2{C}_2$ háromszög tartozik, akkor ezek egyikének minimális, másikának pedig maximális területe van.   (Szmodics Hildegárd, Kaposvár.)   Jegyzet. Az $1^{\circ }$ alatt kimutatott tétel a tér bármely $P$ pontjára is érvényes.   A feladatot még megoldották: Bartók I., Bayer B., Dömény I., Hirschfeld Gy., Kertész F., Kertész G., König D., Lázár L., Pilczer P., Pivnyik I., Póka Gy., Riesz M., Riesz K., Schmidl I., Simon S., Sümegi Gy., Tóbiás I. L.