Kezdőlap


Feladat:	842. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Aczél F. , Bartók I. , Bayer B. , Bogdán G. , Dessauer Antal , Kalmár S. , Kamenitzky M. , Korn A: , König D. , Lamparter J. , Lázár L. , Messik G. , Papp F. , Perlesz D. , Pintér M. , Póka Gy. , Sasvári J. , Schlesinger A. , Schmidl I. , Spitzer V. , Stromfeld F. , Szmodics H. , Tóbiás J. L. , Weisz P. , Wohlstein S.
Füzet:	1901/szeptember, 26 - 27. oldal		PDF \| MathML
Témakör(ök):	Körülírt kör, Terület, felszín, Szögfüggvények, síkgeometriai számítások, Beírt háromszög, Feladat
Hivatkozás(ok):	Feladatok: 1900/szeptember: 842. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen az $A B C$ háromszög köré írt körnek középpontja $O$ ; húzzuk meg az $O C = A O = O B = r$ sugarakat.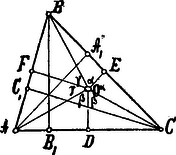

\begin{matrix} A O C Δ = \frac{A C \cdot O D}{2} = \frac{b}{2} \cdot r cos β = \frac{r}{2} b cos β \end{matrix}

\begin{matrix} B O C Δ = \frac{r}{2} a cos α \end{matrix}

\begin{matrix} A O B Δ = \frac{r}{2} c cos γ \end{matrix}

e három egyenletet összeadva:

\begin{matrix} A B C Δ = \frac{r}{2} (a cos α + b cos β + c cos γ), \end{matrix}

a cos α + b cos β + c cos γ = k

a talpponti háromszög kerülete (K. M. L.III. évf. 135. l.), tehát

\begin{matrix} A B C Δ = \frac{r}{2} \cdot k . \end{matrix}

Ha a háromszög derékszögű

(A ∢ = 90^{\circ})

, akkor

\begin{matrix} T = \frac{r}{2} (b cos β + c cos γ), \end{matrix}

\begin{matrix} b cos β + c cos γ = m \end{matrix}

az átfogóra bocsátott merőleges,

r

az átfogónak fele s így

\begin{matrix} T = \frac{r}{2} \cdot 2 m, \end{matrix}

a derékszögű háromszögben a kétszeres magasságot tekinthetjük a talpponti háromszög kerületének s így a képlet itt is érvényes.
A tompaszögű háromszög egyik szöge

> 90^{\circ}

; legyen pl.

γ > 90^{\circ}

, akkor

\begin{matrix} T = \frac{r}{2} (a cos α + b cos β - c cos γ), \end{matrix}

vagyis

\begin{matrix} T = \frac{r}{2} (a_{1} + b_{1} - c_{1}), \end{matrix}

a_{1}, b_{1}, c_{1}

a talpponti háromszög oldalai. (L. K. M. L. III. 135. l. IV. 10. l. IV. 86. l., V. 16. l.)

(Dessauer Antal, Budapest.)

A feladatot még megoldották: Aczél F., Bayer B., Bartók I., Bogdán Gy., Kalmár S., Kamenitzky M., König D., Korn A., Lamparter J., Lázár L., Messik G., Papp F., Perlesz D., Pintér M., Póka Gy., Sasvári J., Schlesinger A., Schmidl I., Spitzer V., Stromfeld F., Szmodics H., Tóbiás J. L., Weisz P., Wohlstein S.