Kezdőlap


Feladat:	831. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Aczél F. , Bayer B. , Bogdán G. , Hirschfeld Gy. , König D. , Lázár L. , Lukhaub Gy. , Mayét J. , Messik G. , Póka Gy. , Sasvári G. , Scharff Jenő , Schlesinger A. , Spitzer V. , Steiner M. , Sümegi Gy. , Tóbiás L. , Wohlstein S.
Füzet:	1901/március, 194 - 195. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Körülírt kör, Beírt kör, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1900/június: 831. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

E feladat megoldása az alkotó részek kiszámítása nélkül a K. M. L. V. évfolyamának 39. oldalán található. Más megoldásai ezek:

1. A körülírható kör középpontjának az oldalaktól való távolságai: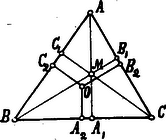

\begin{matrix} O A_{2} = R cos α, O B_{2} = R cos β, O C_{2} = R cos γ \end{matrix}

és így

\begin{matrix} O A_{2} + O B_{2} + O C_{2} = R (cos α + cos β + cos γ) . \end{matrix}

De (lásd a K. M. L. 548. feladatát)

\begin{matrix} cos α + cos β + cos γ = 1 + \frac{r}{R} . \end{matrix}

Eme egyenlőség mindkét oldalát

R

-rel szorozva kapjuk a bizonyítandó tételt.
Ha a háromszög tompaszögű (pl.

γ > 90^{\circ}

), akkor, mivel a tompaszög cosinusa negatív előjelű

\begin{matrix} R (cos α + cos β - cos γ) = O A_{2} + O B_{2} - O C_{2} = R + r . \end{matrix}

2. A 706. feladat alapján :

\begin{matrix} \frac{1}{2} (A M + B M + C M) = R + r . \end{matrix}

A 739. feladat alapján pedig :

\begin{matrix} O A_{2} + O B_{2} + O C_{2} = \frac{1}{2} (A M + B M + C M) . \end{matrix}

E két egyenlet egybevetése a bizonyítandó tételt adja.

(Scharff Jenő. Budapest.)

A feladatot még megoldották: Aczél F., Bayer B., Bogdán G., Hirschfeld Gy., König D, Lázár L., Lukhaub Gy., Mayét J., Messik G., Póka Gy., Sasvári J., Schlesinger A., Spitzer V., Sümegi Gy., Steiner M., Tóbiás L., Wohlstein S.