Kezdőlap


Feladat:	707. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Bertrám J. , Czank K. , Filkorn Jenő , Freibauer E. , Krausz B. , Krisztián Gy. , Lukhaub Gy. , Lupsa Gy. , Messik G. , Messik V. , Oltay K. , Sasvári G. , Szabó J.
Füzet:	1900/február, 123 - 124. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Hossz, kerület, Terület, felszín, Szögfüggvények, síkgeometriai számítások, Szögfelező egyenes, Körülírt kör, Trigonometriai azonosságok, Feladat
Hivatkozás(ok):	Feladatok: 1899/június: 707. matematika feladat

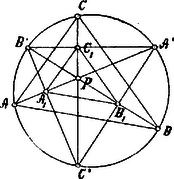
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

(1 $^{\circ})$ Az $A B C$ háromszög belső szögfelezői $P$ pontban metszik egymást.

Az ábra mutatja, hogy

\begin{matrix} A' C' C ∢ + C C' B' ∢ + B B' C' ∢ = A' A C ∢ + C B B' ∢ + B C C' ∢ = \end{matrix}

\begin{matrix} = \frac{α}{2} + \frac{β}{2} + \frac{γ}{2} = 90^{\circ} \end{matrix}

s így

\begin{matrix} C' B_{1} B' ∢ = 90^{\circ} . \end{matrix}

Minthogy továbbá

\begin{matrix} B C' A' ∢ = B A A' ∢ = \frac{α}{2} = A' A C ∢ = A' C' C ∢, \end{matrix}

azért

\begin{matrix} B B_{1} = P B_{1}, \end{matrix}

vagyis

\begin{matrix} P B = 2 P B_{1}; \end{matrix}

hasonlóképp

\begin{matrix} P A = 2 P A_{1} és P C = 2 P C_{1} . \end{matrix}

Minthogy tehát az

A_{1}, B_{1}, C_{1}

pontok az

A P, B P, C P

távolságokat ugyanazon arányban osztják, azért

A B : B C : C A = A_{1} B_{1} : B_{1} C_{1} : C_{1} A_{1}

s így

A B C ▵ \sim A_{1} B_{1} C_{1} ▵

. Ennélfogva

\begin{matrix} K = A B + A C + B C = 2 A_{1} B_{1} + 2 A_{1} C_{1} + 2 B_{1} C_{1} = 2 K_{1}, \end{matrix}

miből

\begin{matrix} K_{1} = \frac{1}{2} K . \end{matrix}

Hasonlóképp:

\begin{matrix} K_{2} = \frac{1}{2} K_{1}, K_{3} = \frac{1}{2} K_{2}, ... \end{matrix}

s így az

A B C, A_{1} B_{1} C_{1}, A_{2} B_{2} C_{2}, ...

háromszögek kerületeinek összege:

\begin{matrix} S_{1} = \frac{K}{1 - \frac{1}{2}} = 2 K . \end{matrix}

Minthogy továbbá

\begin{matrix} T : T_{1} = {\bar{A B}}^{2} : {\bar{A_{1} B_{1}}}^{2} = 4 {\bar{A_{1} B_{1}}}^{2} : {\bar{A_{1} B_{1}}}^{2} = 4 : 1, \end{matrix}

azért

\begin{matrix} T_{1} = \frac{1}{4} T, \end{matrix}

hasonlóképp

\begin{matrix} T_{2} = \frac{1}{4} T_{1}, T_{3} = \frac{1}{4} T_{2}, ... \end{matrix}

a miért is az említett háromszögek területeinek összege:

\begin{matrix} S_{2} = \frac{T}{1 - \frac{1}{4}} = \frac{4}{3} T . \end{matrix}

^{\circ})

A 275. feladat alapján (K.M.L.IV.100.l.)

\begin{matrix} T = 2 R^{2} sin α sin β sin γ, \end{matrix}

ennélfogva

\begin{matrix} T' = 2 R^{2} sin \frac{1}{2} (β + γ) s i n \frac{1}{2} (α + γ) sin \frac{1}{2} (α + β) = \end{matrix}

\begin{matrix} = 2 R^{2} cos \frac{α}{2} cos \frac{β}{2} cos \frac{γ}{2}, \end{matrix}

s így

\begin{matrix} \frac{T}{T'} = \frac{sin α sin β sin γ}{cos \frac{α}{2} cos \frac{β}{2} cos \frac{γ}{2}} = \end{matrix}

\begin{matrix} = \frac{2 sin \frac{α}{2} cos \frac{α}{2} \cdot 2 sin \frac{β}{2} cos \frac{β}{2} \cdot 2 sin \frac{γ}{2} cos \frac{γ}{2}}{cos \frac{α}{2} cos \frac{β}{2} cos \frac{γ}{2}} . \end{matrix}

\begin{matrix} = 8 sin \frac{α}{2} sin \frac{β}{2} sin \frac{γ}{2} . \end{matrix}

^{\circ})

\begin{matrix} r : r' = \frac{T}{s} : \frac{T'}{s'} = \frac{\frac{a b c}{4 R}}{a + b + c} : \frac{\frac{a' b' c'}{4 R}}{a' + b' + c'} = \end{matrix}

\begin{matrix} = a b c (a' + b' + c') : a' b' c' (a + b + c) . \end{matrix}

(Filkorn Jenő, Nyitra.)

A feladatot még megoldották: Bertrám J., Czank K., Freibauer E., Krausz B., Krisztián Gy., Lukhaub Gy., Lupsa Gy., Messik G., Messik V., Oltay K., Sasvári G., Szabó J.