Kezdőlap


Feladat:	630. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Antal Márkus , Freibauer E. , Kornis Ö. , Krausz B. , Krisztián Gy. , Lukhaub Gy. , Sasvári G.
Füzet:	1899/március, 118 - 120. oldal		PDF \| MathML
Témakör(ök):	Simson-egyenes, Feuerbach-kör, Síkgeometriai számítások trigonometria nélkül háromszögekben, Magasságpont, Körülírt kör, Középponti és kerületi szögek, Trapézok, Húrnégyszögek, Háromszögek hasonlósága, Feladat
Hivatkozás(ok):	Feladatok: 1898/december: 630. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{\circ}$ . (2. ábra.) Mérjük rá a $B_{1} D$ távolságra a $P B_{1}$ távolságot úgy, hogy $P B_{1} = B_{1} K$ legyen s hosszabbítsuk meg a $B F$ magasságot $G$ -ig.

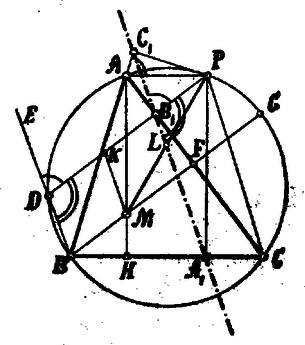2. ábra

Minthogy

M F = F G

,^{$^{*}$} azért

K P G M

egyenlőszárú trapéz;

D P ∥ B G

és

D B = P G

s így

B D P G

is egyenlőszárú trapéz. De az előbbeniek (III. bizonyítás) értelmében

B D ∥ C_{1} A_{1}

s így

K M

is párhuzamos

C_{1} A_{1}

-gyel. Minthogy tehát a Simson-féle egyenes párhuzamos

K M

-mel s felezi a

P K

távolságot, azért a

P K M

háromszög

P M

oldalát is felezi, vagyis keresztül megy ezen egyenesenek

L

középpontján.

2^{\circ}

. (3. ábra.) Legyenek a

P_{1}

és

P_{2}

pontokból az oldalakra bocsátott merőlegesek talppontjai

A_{1}, A_{2}, B_{1}, B_{2}, C_{1}, C_{2},

s_{1}

és

s_{2}

Simson-féle egyenesek metszéspontja

S

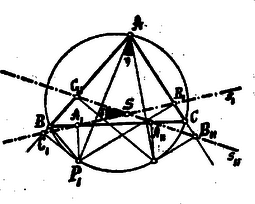3. ábra

A tétel a következőképp bizonytható:
A

P_{1} A_{1} B C_{1}

és a

P_{1} B_{1} A C_{1}

húrnégyszögek, s így

\begin{matrix} C A P_{1} ∢ = B_{1} C_{1} P_{1} ∢ = A_{1} B P_{1} ∢ = α + γ - (90^{\circ} - B A_{1} C ∢), \end{matrix}

tehát

\begin{matrix} B A P_{1} ∢ = α - C A P_{1} ∢ = 90^{\circ} - γ - B A_{1} C_{1} ∢ \end{matrix}

(1)

hasonló eljárás után a

P_{2} B_{2} C A_{2}

és a

P_{2} B_{2} A C_{2}

húrnégyszögekből kapjuk, hogy

\begin{matrix} C A P_{2} ∢ = α - B A P_{2} ∢ = 90^{\circ} - β - C A_{2} B_{2} ∢ \end{matrix}

(2)

Az (1)-et és (2)-őt tekintetbe véve, felírhatjuk, hogy

\begin{matrix} η = P_{1} A P_{2} ∢ = α - B A P_{1} ∢ + C A P_{2} ∢) = (α + β + γ) - 180^{\circ} + B A_{1} C_{1} ∢ + C A_{2} B_{2} ∢) \end{matrix}

vagy

\begin{matrix} η = B A_{1} C_{1} ∢ + C A_{2} B_{2} ∢ \end{matrix}

(3)

Ámde az

s_{1}

és

s_{2}

által bezárt

δ

szög külszöge az

A_{1} S A_{2}

háromszögnek, s így

\begin{matrix} δ = B A_{1} C_{1} ∢ + C A_{2} B_{2} ∢ . \end{matrix}

(4)

A (3) és (4) alapján közvetlenül látható, hogy

\begin{matrix} δ = η . \end{matrix}

3^{\circ}

. (4. ábra.) Kössük össze a változó átmérő

P_{1}

és

P_{2}

végpontjait

M

-mel, a háromszög magasságpontjával s jelöljük

P_{1} M

és

P_{2} M

metszéspontjait az

s_{1}

és

s_{2}

Simson-féle egyenesekkel

S_{1}

és

S_{2}

-vel. Legyen a háromszög köré írható kör középpontja

O

s végre az

S_{1} S_{2}

és

O M

egyenesek metszéspontja

F

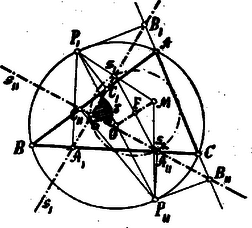4. ábra

Az előbbeniek alapján:

\begin{matrix} δ = 90^{\circ}, P_{1} S_{1} = S_{1} M, P_{2} S_{2} = S_{2} M, \end{matrix}

s minthogy

\begin{matrix} P_{1} O = P_{2} O, \end{matrix}

azért az

M S_{1} S_{2}

és

M P_{1} P_{2}

háromszögek hasonlók. De ekkor:

\begin{matrix} M F = O F \end{matrix}

Látjuk, hogy

F

középpontja ama egyenesnek, mely a magassági pontot a háromszög köré írható kör középpontjával összeköti, miért is

F

a Feuerbach-féle kör középpontja (V. évfolyam 22. lap). Minthogy továbbá

S_{1} S_{2} = \frac{r}{2}

és

δ = 90^{\circ}

, azért

S_{1} S_{2}

a Feuerbach-féle kör átmérője és a Simson-féle egyenesek metszéspontjának,

S

-nek, a mértani helye a Feuerbach-féle kör (IV. 46. lap).

(Antal Márkus.)

A feladatot még megoldották: Freibauer E., Krisztián Gy., Kornis Ö., Krausz B., Lukhaub Gy., Sasvári G.

^{$^{*}$}Jegyzet.

C A H ∢ = C B F ∢

, mert mindkét szög a

B C A

szöget

90^{\circ}

-ra egészíti ki;

C B F ∢ = C B G ∢ = C A G ∢

, mert a

G C

ívhez tartozó kerületi szögek egyenlők. Így tehát

C A H ∢ = C A G ∢

, de

M G ⊥ A C

, miért is

M F = F G