Feladat:	544. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Frankl J. ,  Groffits G. ,  Krisztián György ,  Lukhaub Gy. ,  Prohászka J.
Füzet:	1899/március, 138 - 141. oldal		PDF  |  MathML
Témakör(ök):	Térfogat, Ellipszis, mint mértani hely, Körérintési szerkesztések, Tengely körüli forgatás, Háromszögek hasonlósága, Pitagorasz-tétel alkalmazásai, Szögfüggvények a térben, Szélsőérték-feladatok differenciálszámítás nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1898/június: 544. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.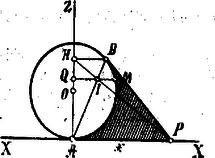   Az $ABH$ és $APO$ háromszögek hasonlóságából következik, hogy $\begin{array}{c}{\displaystyle \frac{AH}{x}=\frac{HB}{r}=\frac{AB}{OP}=\frac{AB\cdot OP}{\overline{O{P}^2}}\mathrm{.}}\end{array}$ De s így $\begin{array}{c}{\displaystyle AH=\frac{2r{x}^2}{r^2+x^2}\mathrm{,}HB=\frac{2r^{2}x}{r^2+x^2}\mathrm{,}AB=\frac{2rx}{\sqrt[]{r^2+x^2}}\mathrm{.}}\end{array}$ $1^{\circ }$ A $PAMB$ idom forgása által keletkezett test köbtartalma $\left(v_1\right)$ egyenlő az $APBH$ és $AMBH$ idomok forgása által keletkezett testek köbtartalmainak külömbségével; tehát $\begin{array}{c}{\displaystyle v_1=\frac{1}{3}\pi AH\left(x^2+x\cdot HB+{\overline{HB}}^2\right)-\pi {\overline{AH}}^2\left(r-\frac{AH}{3}\right)\mathrm{.}}\end{array}$ A fentebb talált értékeket helyettesítve s a kijelölt műveleteket elvégezve, kapjuk, hogy $\begin{array}{c}{\displaystyle v_1=\frac{2\pi r{x}^4}{3\left(r^2+x^2\right)}\mathrm{.}}\end{array}$ Az $APH$ háromszög forgása által keletkezett test köbtartalma $\begin{array}{c}{\displaystyle v_2=\frac{x^2\pi }{3}\cdot AH=\frac{2\pi r{x}^4}{3\left(r^2+x^2\right)}\mathrm{.}}\end{array}$ Látjuk, hogy $v_1=v_2$. A $PBH$ háromszög forgása által keletkezett test köbtartalma egyenlő az $APBH$ és $APH$ idomok forgása által keletkezett testek köbtartalmainak külömbségével. A számításokat elvégezve, azt találjuk, hogy e köbtartalom egyenlő az $AMBH$ idom forgása által keletkezett gömbi segmentum köbtartalmával. $2^{\circ }$ A feltétel szerint $\begin{array}{c}{\displaystyle \frac{2\pi r{x}^4}{3\left(r^2+x^2\right)}:\frac{12\pi r^5{x}^4+4\pi r^3{x}^6}{3{\left(r^2+x^2\right)}^3}=\frac{{\left(r^2+x^2\right)}^2}{2r^2\left(3r^2+x^2\right)}=n\mathrm{,}}\end{array}$ miből $\begin{array}{c}{\displaystyle x=\sqrt[]{r^2\left(n-1\right)+\sqrt[]{r^4{\left(n-1\right)}^2+r^4\left(6n-1\right)}}}\end{array}$ $\begin{array}{c}{\displaystyle =r\sqrt[]{n-1+\sqrt[]{n^2+4n}}\mathrm{.}}\end{array}$ Ha $n=\frac{4}{3}$, akkor $\begin{array}{c}{\displaystyle x=r\sqrt[]{\frac{1}{3}+\sqrt[]{\frac{16}{9}+\frac{16}{3}}}=r\sqrt[]{3}\mathrm{.}}\end{array}$ $3^{\circ }$ Legyen $HAB\sphericalangle =\frac{\alpha }{2}$, $I$ pontból a $HB$-re bocsátott merőleges talppontja $E$, s végre az $A$ -ban rajzolt átmérő másik végponjta $D$. $BI$ a $PBH$ szögnek felezője, tehát a $HBP$ háromszögnek területe $\begin{array}{c}{\displaystyle T=\frac{BI\cdot HB}{2}\text{sin}\left(R-\frac{\alpha }{2}\right)+\frac{BI\cdot x}{2}\text{sin}\left(R-\frac{\alpha }{2}\right)}\end{array}$ vagy $\begin{array}{c}{\displaystyle AH\cdot HB=BI\cdot \left(HB+x\right)\cdot \text{sin}\left(R-\frac{\alpha }{2}\right)\mathrm{.}}\end{array}$ A megfelelő értékekek helyettesítve: $\begin{array}{c}{\displaystyle BI=\frac{4r^{3}x\sqrt[]{r^2+x^2}}{\left(r^2+x^2\right)\left(3r^2+x^2\right)}}\end{array}$ De $BIE\sphericalangle =\frac{\alpha }{2}$ s így $\begin{array}{c}{\displaystyle EI=HQ=BI\cdot \text{cos}\frac{\alpha }{2}=\frac{4r^3{x}^2}{\left(3r^2+x^2\right)\left(r^2+x^2\right)}}\end{array}$ $HQI▵\sim HAP▵$, tehát $\begin{array}{c}{\displaystyle IQ=\frac{x\cdot HQ}{AH}=\frac{2r^{2}x}{3r^2+x^2}}\end{array}$ $AQI▵\sim AHB▵$, tehát $\begin{array}{c}{\displaystyle AQ=\frac{IQ\cdot AH}{HB}=\frac{2r{x}^2}{3r^2+x^2}}\end{array}$ (1) S minthogy $\begin{array}{c}{\displaystyle DH=\frac{2r{x}^3}{r^2+x^2}\mathrm{,}}\end{array}$ azért $\begin{array}{c}{\displaystyle MQ=\sqrt[]{AQ\left(HQ+HD\right)}=\frac{2r^{2}x\sqrt[]{3}}{3r^2+x^2}}\end{array}$ s így $\begin{array}{c}{\displaystyle IQ:MQ=\frac{2r^{2}x\left(3r^2+x^2\right)}{\left(3r^2+x^2\right)\cdot 2r^{2}x\sqrt[]{3}}=\frac{1}{\sqrt[]{3}}=\text{const}\mathrm{.}}\end{array}$ $MQ$ akkor maximum, ha egyenlő $r$-rel és így $IQ$ maximuma $\frac{r}{\sqrt[]{3}}$. (1)-et tekintetbe véve: $\begin{array}{c}{\displaystyle \frac{2r^2{x}^2}{3r^2+x^2}=\frac{r}{\sqrt[]{3}}\mathrm{,}}\end{array}$ miből $\begin{array}{c}{\displaystyle x=r\sqrt[]{3}\mathrm{.}}\end{array}$ Tehát $IQ$ akkor maximum, ha $x=r\sqrt[]{3}$. Minthogy $MQ$ és $IQ$ aránya állandó, azért $I$ pont mértani helye ellipsis, melynek nagy tengelye $AD$ és kis tengelye $\frac{2r\sqrt[]{3}}{3}$.   (Krisztián György.)   A feladatot még megoldották: Frankl J., Groffits G., Lukhaub Gy., Prohászka J.