Kezdőlap


Feladat:	541. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Krisztián György
Füzet:	1899/január, 89 - 91. oldal		PDF \| MathML
Témakör(ök):	Egyenes, Síkgeometriai szerkesztések, Pitagorasz-tétel alkalmazásai, Pont körre vonatkozó hatványa, Hatványvonal, hatványpont, Síkgeometriai számítások trigonometria nélkül körökben, Feladat
Hivatkozás(ok):	Feladatok: 1898/június: 541. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Feladatunk a következő tételek figyelembe vételével könnyen megoldható:

^{\circ}

. Mindazon pontok mértani helye, melyekre nézve az adott

A

és

B

pontoktól való távolságok négyzeteinek külömbsége állandó, oly egyenes, mely

A B

-re merőleges.

Legyen ugyanis a keresett mértani helynek egyik pontja

P

, akkor

\begin{matrix} {\bar{P A}}^{2} = {\bar{P E}}^{2} + {\bar{A E}}^{2} és {\bar{P B}}^{2} = {\bar{P E}}^{2} + {\bar{B E}}^{2} \end{matrix}

s így

\begin{matrix} {\bar{P A}}^{2} - {\bar{P B}}^{2} = {\bar{A E}}^{2} - {\bar{B E}}^{2} . \end{matrix}

^{\circ}

. Ama körök középpontjainak mértani helye, melyek két adott kört két-két átellenes pontban metszenek, oly egyenes, mely az adott körök centrálisára merőlegesen áll.
Legyenk az adott

A

és

B

körök sugarai

r_{1}, r_{2}

, a keresett mértani helynek egyik pontja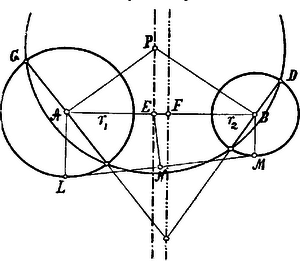

P

Ekkor

\begin{matrix} {\bar{P A}}^{2} - {\bar{P B}}^{2} = {\bar{P G}}^{2} - r_{1}^{2} - {\bar{P D}}^{2} + r_{2}^{2}, \end{matrix}

\begin{matrix} P G = P D \end{matrix}

s így

\begin{matrix} {\bar{P A}}^{2} - {\bar{P B}}^{2} = r_{2}^{2} - r_{1}^{2} . \end{matrix}

A keresett mértani hely az első tétel értelmében tehát csakugyan oly egyenes, mely a két kör centrálisára merőleges; egyúttal látjuk, hogy e mértani hely minden pontjára nézve, a megadott körök középpontjaitól való távolságok négyzeteinek külömbsége egyenlő

r_{2}^{2} - r_{1}^{2}

^{\circ}

. Ismeretes, hogy két kör

(A, B)

hatványvonalának (K-M.L.IV.135.lap) minden

K

pontjára nézve:

\begin{matrix} {\bar{K A}}^{2} - {\bar{K B}}^{2} = r_{1}^{2} - r_{2}^{2} \end{matrix}

s így, ha

F

a hatványvonal s az

A B

centrális metszéspontja, akkor

\begin{matrix} {\bar{F A}}^{2} - {\bar{F B}}^{2} = r_{1}^{2} - r_{2}^{2} . \end{matrix}

Ennek alapján úgy határozhatjuk meg a 2)-ben keresett mértani helynek az

A B

centrálisan fekvő

E

pontját, hogy

A E

-t egyenlővé tesszük

B F

-fel; ekkor ugyanis

\begin{matrix} {\bar{A E}}^{2} - {\bar{B E}}^{2} = {\bar{B F}}^{2} - {\bar{A F}}^{2} = r_{2}^{2} - r_{1}^{2}, \end{matrix}

tehát

E

csakugyan pontja a keresett mértani helynek.
A keresett mértani hely távolsága az egyik kör középpontjától tehát egyenlő a hatványvonalnak távolságával a másik kör középpontjától.

^{\circ}

E

-t a következőképpen is megszerkeszthetjük:

A

és

B

pontokban (2. ábra)

A B

-re merőlegeseket emelünk, melyek a köröket

L

és

M

pontokban metszik. Az

L M

-nek középpontjában emelt merőleges a centrálist a keresett

E

pontban metszi.
Bizonyítás.

\begin{matrix} {\bar{A E}}^{2} - {\bar{B E}}^{2} = {\bar{L E}}^{2} - r_{1}^{2} - {\bar{M E}}^{2} + r_{2}^{2}, \end{matrix}

\begin{matrix} L E = M E \end{matrix}

s így

\begin{matrix} {\bar{A E}}^{2} - {\bar{B E}}^{2} = r_{2}^{2} - r_{1}^{2} . \end{matrix}

^{\circ}

. A keresett mértani hely minden

P

pontja oly tulajdonságú, hogy a két körre vonatkoztatott hatványainak külömsége állandó;

\begin{matrix} ({\bar{P A}}^{2} - r_{1}^{2}) - ({\bar{P B}}^{2} - r_{2}^{2}) = {\bar{P A}}^{2} - {\bar{P B}}^{2} - r_{1}^{2} + r_{2}^{2} = \end{matrix}

\begin{matrix} = r_{2}^{2} - r_{1}^{2} - r_{1}^{2} + r_{2}^{2} = 2 (r_{2}^{2} - r_{1}^{2}) . \end{matrix}

Ez okból e mértani helyet az äquidifferens hatványok vonalának nevezzük.
Ezek alapján feladatunkat a következőképpen oldjuk meg:

A B

-n és

B C

-n a 4)-ben leírt módon meghatározzuk az

E

és

E'

pontokat; az ezen pontokban a centrálisokra emelt merőlegesek a keresett kör középpontjában

O

-ban metszik egymást. E kör sugarát megkapjuk, ha középpontját,

O

-t, az egyik adott kör középpontjával pl.

A

-val összekötjük s

O A

-ra,

A

-ban merőlegest emelünk. A keresett kör ezen átmérőnek két végpontján megy át.

A feladatot megoldotta: Krisztián György.