Feladat: 505. matematika feladat Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Friedmann Bernát ,  Kornis Ö. ,  Krisztián Gy. ,  Riesz Frigyes ,  Sasvári Géza 
Füzet: 1899/január, 87 - 89. oldal  PDF  |  MathML 
Témakör(ök): Simson-egyenes, Síkgeometriai szerkesztések, Húrnégyszögek, Körülírt kör, Kör (és részhalmaza), mint mértani hely, Feladat
Hivatkozás(ok):Feladatok: 1898/március: 505. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Hogy a feladatot megoldhassuk, előre bocsátunk két tételt.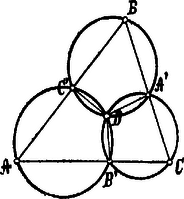
a) A P ponthoz tartozó Simson-féle egyenes (K.M.L.VI.4.sz. 68. lap) a P ponttól és a háromszög magasságpontjától egyenlő távolságra van (K.M.L.III. 54. lap).
b) Ha egy háromszögnek három csúcsán át három kört rajzolunk, melyeknek mindegyike a többi két kört a háromszögnek egy-egy oldalán metszi, akkor a három kör egy pontban metszi egymást.
Bizonyítás. Tegyük föl, hogy a B és A csúcsokon átmenő körök egymást C' és D pontokban metszik; bebizonyítjuk, hogy a harmadik kör is átmegy D ponton.

 

 

A háromszög 3 szöge és a D pont körül fekvő 3 szög ugyanis együttvéve 6R; de BC'DA' és AC'DB' húrnégyszögek s így B∢+C'DA'∢=2R és A∢+C'DB'∢=2R, tehát C∢+B'DA'∢ is 2R, miből következik, hogy CA'DB' is húrnégyszög s ennélfogva a C-n átmenő kör D ponton is átmegy.
E tételből következik, hogy a megadott egyenesek által alkotott háromszögek köré írható körök egy pontban (P) metszik egymást. Az ABF háromszög csúcsain átmenő ADE,BCE és DCF körök az előbbeni tétel értelmében egy P pontban metszik egymást, de a BCE háromszög csúcsain átmenő ABF,BCE és FCD körök is P-ben metszik egymást, tehát P csakugyan közös pontja mind a négy körnek.
Ezek alapján a feladat a következőképpen oldható meg: a megadott egyenesek által alkotott háromszögek köré köröket rajzolunk, melyek a keresett P pontban metszik egymást.
Bizonyítás. A P pontból a CBE háromszög oldalaira bocsátott merőlegesek talppontjai egy egyenesen, a Simson-féle egyenesen feküszenk; épp így az FDC háromszög oldalaira bocsátott merőlegesek talppontjai is egy Simson-féle egyenesen vannak; de minthogy e két egyenesnek két közös pontja van, azért e két egyenes egybeesik s így a négy talppont a négy háromszögnek közös Simson-féle egyenesén fekszik.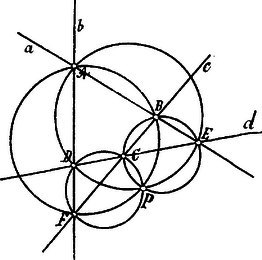
 

 

Minthogy a Simson-féle egyenes a P ponttól és a háromszög magasságpontjaitól egyenlő távolságban van, következik, hogy a háromszögek magassságpontjai csakugyan egy egyenesen vannak, mely egyenes a 4 háromszögnek közös Simson-féle egyenesével párhuzamos.
 
(Sasvári Géza.)

 
II. Megoldás. Azon pontok mértani helye, melyekből valamely háromszög oldalaira bocsátott merőlegesek talppontjai egy s egyenesbe esnek, a háromszög köré írt kör és az s vonalak a háromszög Simson-féle egyenesei. Négy egyenes: a,b,c,d összesen 4 háromszöget alkot, a keresett P pontnak tehát 4 kör kerületén kell feküdnie, a miből egyszersmind azon tétel is következik, hogy 4 egyenes által alkotott háromszögek köré írt körök egymást egy P pontban metszik. Ez a pont felel meg a feladatnak.
Legyenek a háromszögek magasságpontjai M1,M2,M3,M4. A PM távolságokat s, mint Simson-féle egyenes felezi, ennélfogva M1,M2,M3,M4 egy s-sel párhuzamos m egyenesen feküsznek és Pm=2Ps.
Jegyzet. Ismeretes tétel, hogy a parabola gyújtópontjából az érintőkre bocsáott merőlegesek talppontjai a csúcsérintőben feküsznek. Ha tehát a,b,c,d egy parabola érintői, akkor P a parabola gyújtópontja, s egyenes pedig a csúcs tangense. Minthogy Pm-2Ps, m a parabola directrixe. A feladat tehát megadja a négy érintő által adott parabola focusának, csúcstangensének és directrixének szerkesztési módját.
A feladatból folyik még a következő tétel:
A parabola bármely 3 érintője által alkotott háromszög magasságpontja a directrixen fekszik.
Hogy a feladat 4-nél több egyenesre is megoldható legyen, szükséges és elegendő feltétel, hogy ezen egyenesek egy parabola érintői legyenek.
 
(Riesz Frigyes, Zürich.)
 

A feladatot még megoldották: Friedmann Bernát, b.h., Kornis Ö., Krisztián Gy.