Kezdőlap


Feladat:	486. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Devecis M. , Friedmann Bernát , Kántor N. , Riesz F.
Füzet:	1898/szeptember, 19 - 21. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Beírt kör, Súlypont, Középpontos tükrözés, Beírt kör középpontja, Feladat
Hivatkozás(ok):	Feladatok: 1898/február: 486. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Hogy az $A_{1} B_{1} C_{1}$ háromszögben $I'$ -t, mely helyzetére nézve az $A B C$ háromszögben fekvő $I$ -nek felel meg, megtaláljuk, rajzoljunk $A_{1}$ -ből $A T'_{1}$ -tel és $B_{1}$ -ből $B T'_{2}$ -tel párhuzamosokat; e párhuzamosak metszéspontja $I'$ , mert az $A_{1} B_{1} C_{1}$ háromszög megfelelő oldalai is párhuzamosak az $A B C$ háromszög oldalaival. A két háromszögnek közös súlypontja van, mely $A A_{1}$ és $B B_{1}$ metszési pontja.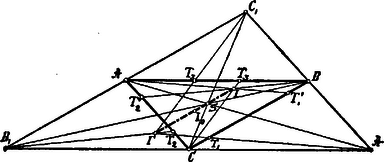

A B I

és

A_{1} B_{1} I'

háromszögek hasonlók, mert megfelelő oldalaik párhuzamosak; ennélfogva:

\begin{matrix} A_{1} I' : A I = A_{1} B_{1} : A B = 2 : 1 \end{matrix}

A_{1} I' ∥ A I

, arányuk

2 : 1

;

A_{1} S ∥ A S

, arányuk ugyanacsak

2 : 1

, miből következik, hogy az

A S I

és

A_{1} S I'

háromszögek hasonlók. E két háromszög hasonlóságából következik a tétel mindkét részének helyessége. Ugyanis: 1

^{\circ}

A S I ∢ = A S I' ∢

, a mi annyit mond, hogy

I, S,

és

I'

pontok egy egyenesbe esnek. Egész hasonlóan bizonyíthatjuk be, hogy

I^{(k)}, I^{(k + 1)}

és

S

pontok is egyenesen vannak. Így tehát egymásután kimutathatjuk, hogy

(I, S, I'), (I', S, I''), ..., (I^{(k)}, S, I^{(k + 1)}, ..., (I^{(n - 11)}, S, I^{(n)}

egy egyenesen vannak, a mivel a tétel első részét bebizonyítottuk.
2

^{\circ}

. Ugyancsak a két háromszög hasonlóságából következik, hogy

\begin{matrix} I' S = 2 I S; \end{matrix}

hasonlóképpen kimutathatjuk, hogy

\begin{matrix} I'' S = 2 I' S = 2^{2} I S; \end{matrix}

Minthogy pedig (K.M.L. 294. feladat IV. évfolyam 167. lap)

\begin{matrix} I S = 2 I_{0} S, \end{matrix}

azért

\begin{matrix} I^{(n)} S = 2^{n + 1} I_{0} S . \end{matrix}

(Friedmann Bernát.)

A feladatot még megoldották: Devecis Mihály, Kántor Nándor (b. h.), Riesz Frigyes (műegyet. h.).