Kezdőlap


Feladat:	464. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bojedain F. , Détshy K. , Devecis M. , Erdős A. , Freibauer E. , Goldziher K. , Kertész L. , Koós A. , Kornis Ö. , Krausz B. , Krisztián Gy. , Manheim Emil , Pollák N. , Porkoláb J. , Probst E. , Roth M. , Sasvári Géza , Spitzer Ö. , Szabó I. , Szabó K. , Weisz J.
Füzet:	1898/április, 164. oldal		PDF \| MathML
Témakör(ök):	Háromszögek szerkesztése, Szögfelező egyenes, Háromszögek egybevágósága, Középponti és kerületi szögek, Egyenlő szárú háromszögek geometriája, Feladat
Hivatkozás(ok):	Feladatok: 1898/január: 464. matematika feladat

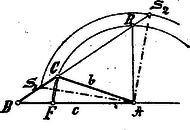
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Legyen $A B C$ a keresett háromszög s messe a belső szögfelező $B C$ -t $S_{1}$ -ben, a külső szögfelező $S_{2}$ -ben. Emeljünk $A B$ oldalnak $A$ pontjában merőlegest, mely $B C$ -t $R$ -ben metszi.

Minthogy

\begin{matrix} A S_{1} = A S_{2}, C S_{1} A ∢ = R S_{2} A ∢ = 45^{\circ}, S_{1} A C ∢ = R A S_{2} ∢ \end{matrix}

azért

\begin{matrix} A S_{1} C ▵ ≅ A R S_{2} ▵ \end{matrix}

s így

\begin{matrix} A C = A R = b . \end{matrix}

Ezek alapján a szerkesztés a következő:

A B = c

oldal egyik végpontjából, mint középpontból

A C = b

sugárral kört rajzolunk.

A

pontban

A B

-re merőlegest emelünk, mely a kört

R

-ben metszi. Az

R

pontot

B

-vel összekötő egyenes a kört a keresett harmadik csúcsban,

C

-ben metszi.

(Sasvári Géza.)

II. Megoldás.

A C = b

-t

A

-ból

A B

-re

F

-ig rámérjük s a

B F

egyenesre, mint húrra, oly kört rajzolunk, melynek a

B F

húron fekvő kerületi szögei

45^{\circ}

-kal egyenlők. E kört az

A

-ból mint középpontból

A C

sugárral rajzolt kör

C

-ben metszi.

A B C

a keresett háromszög.

Bizonyítás.

A C F ▵

egyenlőszárú, tehát

A S_{1} ⊥ C F, C S_{1} A ∢ = 45^{\circ}

s így

S_{1} C F ∢

45^{\circ}

(Manheim Emil.)

A feladatot még megoldották: Bojedain F., Détshy K., Devecis M., Erdős A., Freibauer E., Goldziher K., Kertész L., Koós A., Kornis Ö., Krausz B., Krisztián Gy., Pollák N., Porkoláb J., Probst E., Roth M., Spitzer Ö., Szabó I., Szabó K., Weisz J.