Kezdőlap


Feladat:	444. matematika feladat	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Manheim Emil , Sasvári Géza
Füzet:	1898/március, 143 - 144. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometria nélkül háromszögekben, Háromszögek szerkesztése, Mértani közép, Derékszögű háromszögek geometriája, Aranymetszés, Kör (és részhalmaza), mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1897/december: 444. matematika feladat

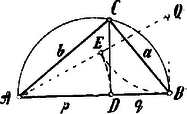
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Legyen az $A B C$ háromszögben $A D = p$ és $D B = q$ .

A feladat értelmében

\begin{matrix} b^{2} = a c \end{matrix}

de egyúttal

\begin{matrix} b^{2} = p c \end{matrix}

s így

\begin{matrix} a = p . \end{matrix}

Minthogy pedig

\begin{matrix} a^{2} = q c \end{matrix}

azért

\begin{matrix} p^{2} = q c . \end{matrix}

Látjuk tehát, hogy a háromszögben, mely a feladat követelményeinek megfelel, a derékszög csúcsából az átfogóra bocsátott merőleges, oly két részre osztja az átfogót, melyek közül a nagyobbik rész mértani középarányos az egész átfogó és a kisebbik rész között. Ily tulajdonságú részekre, mint az ismeretes, az arany metszéssel (sectio aurea, divina) osztjuk az egyenest. Ezek alapján a szerkesztés a következő lesz: A megadott

A B

egyenesre

B

pontban merőlegest emelünk, melyre rámérjük

B Q = \frac{1}{2} A B

-t.

Q

pontból

Q B

sugárral félkört rajzolunk, mely

A Q

-t

E

-ben metszi.

A E

-t lemérjük

A

-tól

A B

-re

D

-ig;

D

-ben

A B

-re merőlegest emelünk, mely a derékszögű háromszög

C

csúcsának egyik mértani helye.

C

másik mértani helyét megkapjuk, ha

A B

fölé félkört rajzolunk.

A B C

a keresett háromszög.

(Manheim Emil.)

II. Megoldás.

\begin{matrix} b^{2} + a^{2} = c^{2} \end{matrix}

és

\begin{matrix} b^{2} = c a \end{matrix}

egyenletekből ered:

\begin{matrix} a^{2} + c a = c^{2} \end{matrix}

miből

\begin{matrix} a = - \frac{c}{2} + \sqrt[]{{(\frac{c}{2})}^{2} + c^{2}}, \end{matrix}

mely kifejezés az I. megoldásban közölt szerkesztésnek teljesen megfelel.

(Sasvári Géza.)

Megoldások száma: 47.