Kezdőlap


Feladat:	416. matematika feladat	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Bobál S. , Bojedain F. , Détshy K. , Devecis M. , Erdős A. , Führer K. , Goldziher K. , Hrivnák A. , Kárf J. , Kertész L. , Kornis Ö. , Probst E. , Roth M. , Schiffer H. , Spitzer Ö. , Szabó I. , Szabó K. , Weisz J.
Füzet:	1898/március, 138. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Súlyvonal, Háromszögek szerkesztése, Derékszögű háromszögek geometriája, Kör (és részhalmaza), mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1897/október: 416. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen az $A B C$ derékszögű háromszög átfogója $A B = c$ , s jelöljük a középvonalakat 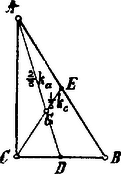$k_{a}, k_{b}$ és $k_{c}$ -vel.
Első eset. Adva van $k_{a} = A D$ és $K_{c} = C E$ .

Minthogy

E

a derékszögű háromszög csúcsain átmenő kör középpontja, azért

A E = C E = k_{c}

. Minthogy továbbá

A G = \frac{2}{3} k_{a}

és

E G = \frac{1}{3} k_{c}

, azért

A G E

háromszög, s így az

A B C

háromszög is megszerkeszthető.
Második eset. Adva van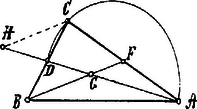

B F = k_{b}

és

A D = k_{a}

A derékszögű háromszög

C

csúcsának egyik mértani helye az

A D = k_{a}

középvonal fölé rajzolt félkör.

A D

meghosszabbítására mérjük rá

D H = G D = \frac{1}{3} k_{a}

-t és kössük össze

H

-t

C

-vel. Minthogy

A F = F C

és

A G = G H

, azért az

A F G

és

A C H

háromszögek hasonlók, s így

C H = 2 F G = \frac{2}{3} k_{b}

. Ennélfogva a

C

pont második mértani helye a

H

-ból mint középpontból

\frac{2}{3} k_{b}

sugárral rajzolt körív.
A szerkesztés tehát a következő: Megrajzoljuk

A D = k_{a}

-t;

A D

-t megnyújtjuk, s

\frac{1}{3} k_{a}

-t mérünk rá, mi által

H

pontot kapjuk.

H

-ból

\frac{2}{3} k_{b}

sugárral kört rajzolunk, mely az

A D

fölé rajzolt félkört

C

-ben metszi.

C

-t összekötjük

A

-val és

D

-vel s végre

C D

meghosszabbítására még egyszer rámérjük

C D

-t, miáltal

B

-t kapjuk.

A feladatot megoldották: Bobál S., Bojedain F., Détshy K., Devecis M., Erdős A., Führer K., Goldziher K., Hrivnák A., Kráf J., Kertész L., Kornis Ö., Probst E., Roth M., Schiffer H., Spitzer Ö., Szabó I., Szabó K., Weisz J.