Kezdőlap


Feladat:	399. matematika feladat	Korcsoport: 18-	Nehézségi fok: könnyű
Megoldó(k):	Bojedain F. , Devecis M. , Fekete Jenő , Fleischmann S. , Petrogalli G. , Probst E. , Spitzer Ö. , Szabó I. , Szabó K.
Füzet:	1897/december, 78 - 79. oldal		PDF \| MathML
Témakör(ök):	Egyenes körkúpok, Térfogat, Gömb és részei, Csonkakúp, Másodfokú (és arra visszavezethető) egyenletek, Térgeometriai számítások trigonometria nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1897/szeptember: 399. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen $D F = a, F G = m$ .
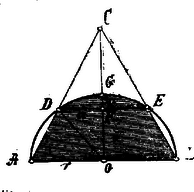
A két testtel közös testrész $V$ köbtartalma egyenlő egy csonka kúp és egy gömbszelet köbtartalmának összegével.

A csonka kúp köbtartalma:

\begin{matrix} V_{1} = \frac{2}{3} r^{3} π - \frac{2}{3} a^{3} π = \frac{2}{3} π (r^{3} - a^{3}) \end{matrix}

(1)

D F O

háromszögből

\begin{matrix} r^{2} = a^{2} + {(2 r - 2 a)}^{2} \end{matrix}

vagy

\begin{matrix} 5 a^{2} - 8 a r + 3 r^{2} = 0, \end{matrix}

miből

\begin{matrix} a = \frac{4 \pm 1}{5} r \end{matrix}

a

-nak két értéke közül csak az egyiket használhatjuk, mert a feladat értelmében

a

nem lehet

r

-el egyenlő; így tehát

a = \frac{3}{5} r

a

-nak ezen értékét (1)-be téve

\begin{matrix} V_{1} = \frac{2}{3} π (r^{3} - \frac{27}{125} r^{3}) = \frac{196}{375} r^{3} π \end{matrix}

(2)

A gömbszelet köbtartalma:

\begin{matrix} V_{2} = m^{2} π (r - \frac{m}{3}) \end{matrix}

hol

\begin{matrix} m = 2 a - r = \frac{6}{5} r - r = \frac{r}{5} \end{matrix}

s így

\begin{matrix} V_{2} = \frac{r^{2} π}{25} (r - \frac{r}{15}) = \frac{14 r^{3} π}{375} \end{matrix}

(3)

A csonka kúp és a gömbszelet köbtartalmát összeadva, kapjuk a keresett köbtartalmat;

\begin{matrix} V = \frac{196}{375} r^{3} π + \frac{14}{375} r^{3} π \end{matrix}

\begin{matrix} V = \frac{210}{375} r^{3} π = \frac{14}{25} r^{3} π . \end{matrix}

(Fekete Jenő.)

A feladatot még megoldották: Bojedain F., Devecis M., Fleischmann S., Petrogalli G., Probst E., Spitzer Ö., Szabó I., Szabó K.