Feladat:	391. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Dénes A. ,  Devecis M. ,  Friedmann Bernát ,  Goldziher K. ,  Grosz A. ,  Kántor N. ,  Kornis Ö. ,  Riesz Frigyes ,  Spitzer Ö. ,  Szabó I. ,  Szabó K. ,  Weisz Á.
Füzet:	1897/december, 74 - 75. oldal		PDF  |  MathML
Témakör(ök):	Ceva-tétel, Menelaosz-tétel, Síkgeometriai számítások trigonometria nélkül háromszögekben, Projektív geometria, Feladat
Hivatkozás(ok):	Feladatok: 1897/szeptember: 391. matematika feladat

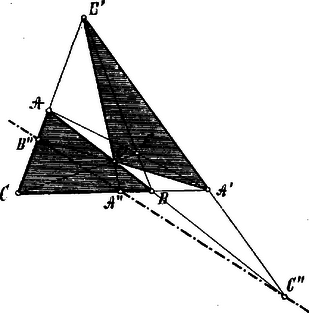
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Az $A\text{'}B\text{'}\mathrm{,}A\text{'}C\text{'}\mathrm{,}B\text{'}C\text{'}$ szelők által metszett $ABC$ háromszögre a Menelaos-féle tételt (K.M.L.IV.148. l.) alkalmazva: $\begin{array}{c}{\displaystyle \frac{BA\text{'}}{CA\text{'}}\cdot \frac{CB\text{'}}{AB\text{'}}\cdot \frac{AC\text{'}\text{'}}{BC\text{'}\text{'}}=\mathrm{1,}}\end{array}$ (1) $\begin{array}{c}{\displaystyle \frac{BA\text{'}}{CA\text{'}}\cdot \frac{CB\text{'}\text{'}}{AB\text{'}\text{'}}\cdot \frac{AC\text{'}}{BC\text{'}}=\mathrm{1,}}\end{array}$ (2) $\begin{array}{c}{\displaystyle \frac{BA\text{'}\text{'}}{CA\text{'}\text{'}}\cdot \frac{CB\text{'}}{AB\text{'}}\cdot \frac{AC\text{'}}{BC\text{'}}=\mathrm{1,}}\end{array}$ (3) A Ceva-féle tétel alapján: $\begin{array}{c}{\displaystyle \frac{CA\text{'}}{BA\text{'}}\cdot \frac{AB\text{'}}{CB\text{'}}\cdot \frac{BC\text{'}}{AC\text{'}}=-1}\end{array}$ (4) (1)-et, (2)-t, (3)-at és (4)-nek négyzetét egymással megszorozva: $\begin{array}{c}{\displaystyle \frac{BA\text{'}\text{'}}{CA\text{'}\text{'}}\cdot \frac{CB\text{'}\text{'}}{AB\text{'}\text{'}}\cdot \frac{AC\text{'}\text{'}}{BC\text{'}\text{'}}=\mathrm{1,}}\end{array}$ mely képlet kriteriuma annak, hogy az $A\text{'}\text{'}B\text{'}\text{'}C\text{'}\text{'}$ pontok egy egyenesben fekszenek. A tétel megfordítható. A feladat megoldását a 155. feladat is tartalmazza; ha ugyanis két háromszög, $ABC$ és $A\text{'}B\text{'}C\text{'}$ ugyanazon betűvel jelzett csúcsainak összekötő egyenesei egy pontban találkoznak, akkor ugyanazon betűvel jelzett oldalak metszéspontjai egy egyenesben feküsznek és megfordítva.   (Riesz Frigyes, műegyetemi hallgató, Zürich.)   A feladatot még megoldották: Friedmann B., Grosz A., Kántor N. egyetemi hallgatók; továbbá Dénes A., Devecis M., Goldziher K., Kornis Ö., Spitzer Ö., Szabó I., Szabó K., Weisz A.