Kezdőlap


Feladat:	370. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Friedmann Bernát , Kornis Ödön , Riesz Frigyes
Füzet:	1898/január, 92 - 95. oldal		PDF \| MathML
Témakör(ök):	Körülírt kör, Beírt kör, Feuerbach-kör, Szögfüggvények, síkgeometriai számítások, Hozzáírt körök, Középponti és kerületi szögek, Derékszögű háromszögek geometriája, Trigonometriai azonosságok, Feladat
Hivatkozás(ok):	Feladatok: 1897/június: 370. matematika feladat

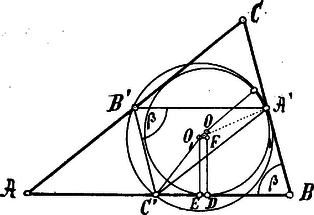
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1 $^{\circ}$ . Tudjuk, hogy a Feuerbach-féle kör ^{$^{*}$} keresztül megy az $A', B',$ és $C'$ oldalfelező pontokon.

Legyen

O_{1}

a Feuerbach-féle kör középpontja,

O_{1} C' = \frac{R}{2}

a sugara, hol

R

A B C

háromszög köré írt kör sugara; legyen továbbá a háromszöget belül érintő kör középpontja

O

, sugara

O D = r

; a háromszög oldalai

a, b, c

; szögei

α, β, γ

; a háromszög félkerülete

s

\begin{matrix} O_{1} C' B' ∢ = O_{1} C' A' ∢ + A' C' B ∢ \end{matrix}

C' O_{1} A' ∢

mint középponti szög

2 β

, tehát

O_{1} C' A' ∢ = 90^{\circ} - β

A' C' B' ∢ = α

, mert

A' D' ∥ A C

s így

\begin{matrix} O_{1} C' B' ∢ = 90^{\circ} - (β - α) . \end{matrix}

O O_{1} F

derékszögű háromszögből az

O O_{1}

centrális négyzete:

\begin{matrix} {\bar{O O_{1}}}^{2} = {\bar{O F}}^{2} + {\bar{O_{1} F}}^{2} . \end{matrix}

(1)

\begin{matrix} O F = O D - O_{1} E = r - \frac{R}{2} cos (β - α) \end{matrix}

és

\begin{matrix} O_{1} F = E D = C' B - B D - C' E \end{matrix}

\begin{matrix} \frac{c}{2} - (s - b) - \frac{R}{2} sin (β - α) = \frac{b - a}{2} - \frac{R}{2} sin (β - α) \end{matrix}

\begin{matrix} = R (sin β - sin α) - \frac{R}{2} sin (β - α) \end{matrix}

s így

\begin{matrix} {\bar{O O_{1}}}^{2} = {[r - \frac{R}{2} cos (β - α)]}^{2} + {[R (sin β - sin α) - \frac{R}{2} sin (β - α)]}^{2} \end{matrix}

\begin{matrix} {\bar{O O_{1}}}^{2} = r^{2} \frac{R^{2}}{4} - R r cos (β - α) + R^{2} (sin β - sin α) \times \end{matrix}

\begin{matrix} \times [(sin β - sin α) - sin (β - α)] \end{matrix}

\begin{matrix} cos (β - α) = 1 - 2 sin^{2} \frac{β - α}{2} \end{matrix}

s így

\begin{matrix} {\bar{O O_{1}}}^{2} = r^{2} + \frac{R^{2}}{4} - R r + 2 R r sin^{2} \frac{β - α}{2} + 4 R^{2} cos \frac{β - α}{2} + 4 R^{2} cos \frac{β + α}{2} sin^{2} \frac{β - α}{2} \times \end{matrix}

\begin{matrix} \times (cos \frac{β + α}{2} - cos \frac{β - α}{2}) \end{matrix}

\begin{matrix} = {(r - \frac{R}{2})}^{2} + 2 R r sin^{2} \frac{β - α}{2} - 8 R^{2} sin^{2} \frac{β - α}{2} sin \frac{α}{2} sin \frac{β}{2} sin \frac{γ}{2} . \end{matrix}

Minthogy pedig

\begin{matrix} 4 R sin \frac{α}{2} sin \frac{β}{2} sin \frac{γ}{2} = r \end{matrix}

azért

\begin{matrix} {\bar{O O_{1}}}^{2} = {(r - \frac{R}{2})}^{2} + 2 R r sin^{2} \frac{β - α}{2} - 2 R r sin^{2} \frac{β - α}{2} \end{matrix}

vagyis

\begin{matrix} O O_{1} = \frac{R}{2} - r . \end{matrix}

Minthogy tehát a centrális egyenlő a két kör sugarának különbségével, azért a két kör egymást csakugyan belülről érinti.

^{\circ}

. Legyen a háromszöget kívülről érintő körök egyikének középpontja

O_{2}

, sugara

O_{2} D_{1} = r_{1}

O_{1} F_{1} O_{2}

derékszögű háromszögből az

O_{1} O_{2}

centralis négyzete:

\begin{matrix} {\bar{O_{1} O_{2}}}^{2} = {\bar{O_{2} F_{1}}}^{2} + {\bar{O_{1} F_{1}}}^{2} . \end{matrix}

(2)

\begin{matrix} O_{2} F_{1} = O_{2} D_{1} + O_{1} E = r_{1} + \frac{R}{2} cos (β - α) \end{matrix}

és

\begin{matrix} O_{1} F_{1} = E D_{1} = C' A - A D_{1} + C' E . \end{matrix}

Minthogy pedig

\begin{matrix} A D_{1} = B D = s - b, \end{matrix}

azért

\begin{matrix} O_{1} F_{1} = \frac{c}{2} - (s - b) + \frac{R}{2} sin (β - α) \end{matrix}

\begin{matrix} = \frac{b - a}{2} + \frac{R}{2} sin (β - α) \end{matrix}

\begin{matrix} = R (sin β - sin α) + \frac{R}{2} sin (β - α) \end{matrix}

s így

\begin{matrix} {\bar{O_{1} O_{2}}}^{2} = {[r_{1} + \frac{R}{2} cos (β - α)]}^{2} + {[R (sin β - sin α) - \frac{R}{2} sin (β - α)]}^{2} \end{matrix}

\begin{matrix} = r_{1}^{2} + \frac{R^{2}}{4} + R r_{1} cos (β - α) + R^{2} (sin β - sin α) \times \end{matrix}

\begin{matrix} \times [(sin β - sin α) + sin (β - α)] \end{matrix}

\begin{matrix} = r_{1}^{2} + \frac{R^{2}}{4} + R r_{1} - 2 R r_{1} sin^{2} \frac{β - α}{2} + 4 R^{2} cos \frac{β + α}{2} sin^{2} \frac{β - α}{2} \times \end{matrix}

\begin{matrix} \times (cos \frac{β + α}{2} - cos \frac{β - α}{2}) \end{matrix}

\begin{matrix} = {(r_{1} + \frac{R}{2})}^{2} - 2 R r_{1} sin^{2} \frac{β - α}{2} + 8 R^{2} sin^{2} \frac{β - α}{2} cos \frac{α}{2} \times \end{matrix}

\begin{matrix} \times cos \frac{β}{2} sin \frac{γ}{2} . \end{matrix}

Minthogy pedig

\begin{matrix} 4 R cos \frac{α}{2} cos \frac{β}{2} sin \frac{γ}{2} = r_{1} \end{matrix}

azért

\begin{matrix} {\bar{O_{1} O_{2}}}^{2} = {(r_{1} + \frac{R}{2})}^{2} - 2 R r_{1} sin^{2} \frac{β - α}{2} + 2 R r_{1} sin^{2} \frac{β - α}{2} \end{matrix}

vagyis

\begin{matrix} O_{1} O_{2} = r_{1} + \frac{R}{2} . \end{matrix}

Minthogy tehát a centrális a két kör sugarának összegével egyenlő, a két kör egymást kívülről érinti. Ugyanezt hasonlóképp kimutathatjuk a másik két kívülről érintő körről is.

(Friedmann Bernát.)

A feladatot még megoldották: Riesz Frigyes műegyetemi hallgató és Kornis Ödön.

^{$^{*}$}Azon kört, mely a háromszög magasságainak talppontjain, az oldalak középpontjain és a magasságoknak a csúcsok felé eső részeinek középpontjain megy át, Feuerbach-féle körnek nevezzük (K.M.L, A talpponti háromszög; IV. 44. lap.).