Kezdőlap


Feladat:	305. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Devecis M. , Eisltzer Gy. , Friedmann B. , Grünhut B. , Kornis Ö. , Kunsch M. , Preisz Károly , Riesz F. , Suschnik J. , Visnya Aladár , Weisz Lipót
Füzet:	1897/június, 170 - 171. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometria nélkül háromszögekben, Síkgeometriai számítások trigonometria nélkül körökben, Körülírt kör, Beírt háromszög, Egyenlő szárú háromszögek geometriája, Háromszögek egybevágósága, Tengelyes tükrözés, Szögfelező egyenes, Feladat
Hivatkozás(ok):	Feladatok: 1897/január: 305. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Segédtétel: A háromszög köré írható körnek a csúcsokhoz vont sugarai merőlegesek a talpponti háromszög oldalaira.
Húzzuk meg pl. $A O Q$ átmérőt, mely a talpponti háromszög $B_{1} C_{1}$ oldalát $P$ -ben metszi.

\begin{matrix} A Q C ∠ = A B C ∠ = β \end{matrix}

tehát, mivel

A C Q

derékszög,

P A B_{1} ∠ = 90^{\circ} - β

és (K.M.L. IV. évf. A talpponti háromszög 2.)

A B_{1} C_{1} ∠ = β, O A

valóban merőleges

B_{1} C_{1}

-re.

(Suschnik József, műegyetemi hallgató.)

I. Megoldás. A kérdéses szeletek

C_{1} P

és

P B_{1}

, ha tehát

C'_{1}

C_{1}

tükörképe

O A

-ra nézve, úgy külömbségük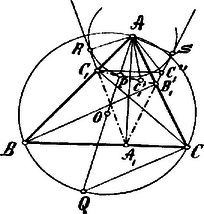

B_{1} C'_{1}

Ha most

C_{1}

-ből merőlegest bocsátunk

A A_{1}

-re, mely

A_{1} B_{1}

-et

C_{1}''

-ben metszi, akkor, mivel

A A_{1}

egyidejűleg magassága és szögfelezője

C_{1} A C''_{1}

háromszögnek, ez egyenlőszárú és

B_{1} C'_{1}

nem más, mint az

A_{1} C_{1}

és

A_{1} B_{1}

oldalok külömbsége. Hogy tehát bebizonyítsuk, hogy

B_{1} C'_{1} = B_{1} C''_{1}

, az

A B_{1} C_{1}'

és

A B_{1} C''_{1}

háromszögek egybevágóságát fogjuk kimutatni.

A B_{1}

oldal közös,

A B_{1} C'_{1} ∠ = A B_{1} C''_{1} ∠

és

A C_{1}' = A C''_{1}

, mert

C_{1} A C'_{1}

háromszög egyenlőszárúságából

A C'_{1} = A C'_{1}

és

A C_{1} A_{1}

és

A C_{1}'' A_{1}

háromszögek egybevágóságából (két oldal és a közbe zárt szög)

A C_{1}''

szintén egyenlő

A C_{1}

-gyel.

(Weisz Lipót.)

II. Megoldás. A segédtétel értelmében a köré írható kör középpontjából a talpponti háromszög oldalaira bocsátott merőlegesek átmennek a csúcsokon, és így, mivel a háromszög oldalai a talpponti háromszög külső szögfelezői, a csúcsok a talpponti háromszöget kívülről érintő köreinek középpontjai és a szóban forgó merőlegesek talppontjai az érintési pontok. Ha az

A

körül írt kör másik két érintési pontja

R

és

S

úgy

\begin{matrix} A_{1} R = A_{1} S \end{matrix}

\begin{matrix} A_{1} C_{1} + C_{1} R = A_{1} B_{1} + B_{1} S . \end{matrix}

\begin{matrix} C_{1} R = C_{1} P \end{matrix}

és

\begin{matrix} B_{1} S = B_{1} P \end{matrix}

tehát

\begin{matrix} A_{1} C_{1} + C_{1} P = A_{1} B_{1} + B_{1} P \end{matrix}

a honnan

\begin{matrix} A_{1} C_{1} - A_{1} B_{1} = B_{1} P - C_{1} P \end{matrix}

(Preisz Károly.)

III. Megoldás. Legyen

A_{1}

-nek a

c

oldalra vonatkozó tükörképe

P

és a

b

oldalra vonatkozó tükörképe

Q

, akkor, mivel a háromszög oldalai a talpponti háromszög külső szögfelezői,

P

és

Q

B_{1} C_{1}

egyenesre esnek és

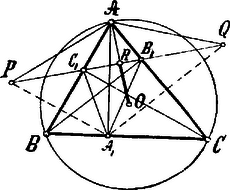\begin{matrix} P C_{1} = A_{1} C_{1}, B_{1} Q = A_{1} B_{1} . \end{matrix}

(1)

Az ily módon keletkezett

P A Q

háromszög egyenlőszárú, mert

A P

és

A Q

A A_{1}

-nek tükörképei, és mivel a segédtétel értelmében

O R

merőleges átmegy az

A

csúcson,

R

e háromszög magasságának talppontja, mely az alapot felezi. Tehát

\begin{matrix} P C_{1} + C_{1} R = R B_{1} + B_{1} Q . \end{matrix}

Az (1) alatti értéket betéve

\begin{matrix} A_{1} C_{1} + C_{1} R = R B_{1} + A_{1} B_{1}, \end{matrix}

a honnan csakugyan

\begin{matrix} C_{1} R - R B_{1} = A_{1} B_{1} - A_{1} C_{1} . \end{matrix}

(Visnya Aladár.)

A feladatot még megoldották: Devecis M., Eislitzer Gy., Friedmann B., Grünhut B., Kornis Ö., Kunsch M., Riesz F., Suschnik J.