Kezdőlap


Feladat:	294. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Visnya Aladár , Weisz Lipót
Füzet:	1897/június, 167 - 170. oldal		PDF \| MathML
Témakör(ök):	Menelaosz-tétel, Szögfelező egyenes, Súlypont, Síkgeometriai számítások trigonometria nélkül háromszögekben, Szögfüggvények, síkgeometriai számítások, Háromszögek hasonlósága, Érintőnégyszögek, Feladat
Hivatkozás(ok):	Feladatok: 1896/december: 294. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{\circ} .$ Tegyük fel, hogy az $A_{1}, B_{1}$ és $C_{1}$ pontok egy egyenesbe esnek; bizonyítsuk be, hogy az $A_{2}, B_{2}$ és $C_{2}$ pontok is egy egyenesbe esnek, föltéve, hogy az $A_{1}, A_{2},$ a $B_{1}, B_{2}$ és $C_{1}, C_{2}$ pontok a megfelelő oldalt felező ponthoz képest symmetrikusan feküsznek.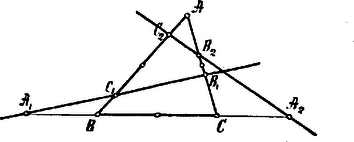

Miután az

A_{1}, B_{1}

és

C_{1}

pontok egy egyenesbe esnek, a Menelaos-féle tétel értelmében:

\begin{matrix} \frac{A_{1} C}{A_{1} B} \cdot \frac{C_{1} B}{C_{1} A} \cdot \frac{B_{1} A}{B_{1} C} = 1 \end{matrix}

De a föltétel szerint:

\begin{matrix} A_{1} B = A_{2} C, A_{1} C = A_{2} B, B_{1} C = B_{2} A, B_{1} A = B_{2} C, C_{1} A = C_{2} B, C_{1} B = C_{2} A \end{matrix}

tehát

\begin{matrix} \frac{A_{2} C}{A_{2} B} \cdot \frac{C_{2} B}{C_{2} A} \cdot \frac{B_{2} A}{B_{2} C} = 1 \end{matrix}

a mi azt mondja, hogy az

A_{2}, B_{2}

és

C_{2}

pontok szintén egy egyenesbe esnek.

2^{\circ} .

Legyenek az

A B C

háromszög oldalai

a, b

és

c

;

C_{2} B_{2}

az egyik egyenes, mely a háromszögbe írható kört

T

pontban érinti,

C_{1} B_{1}

a másik egyenes. Húzzunk az

A B C

háromszög csúcsain keresztül a szemközt fekvő oldalakkal párhuzamosokat; ez által az

A' B' C'

háromszöget nyerjük, mely

A B C

háromszöghöz hasonló; belső hasonlósági pontjuk

S

-ben, a két háromszög közös súlypontjában van. Legyen

C_{1} B_{1}

-nek

A' C'

, illetőleg

A' B'

-tel való metszéspontja

R

, illetőleg

N

. Vonjunk

M

ponton keresztül

R N

-nel párhuzamost és legyen e párhuzamosnak az

A C

, illetőleg

A B

oldalakkal való metszéspontja

R_{1}

, illetőleg

N_{1}

. Legyen végre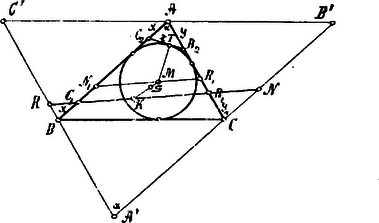

\begin{matrix} B C_{1} = A C_{2} = x, C B_{1} = A B_{2} = y \end{matrix}

B_{1} C N

és

B_{1} A C_{1}

háromszögek hasonlóságából következik, hogy:

\begin{matrix} \frac{C N}{c - x} = \frac{y}{b - y} \end{matrix}

honnan

\begin{matrix} C N = \frac{y (c - x)}{b - y} \end{matrix}

és így

\begin{matrix} A' N' = A' C + C N = c + \frac{y (c - x)}{b - y} = \frac{b c - x y}{b - y} \end{matrix}

(1)

Hasonlóképpen levezethető, hogy:

\begin{matrix} A' R = \frac{b c - x y}{c - x} \end{matrix}

De az

A' N R

háromszögnek az

N R

oldalhoz tartozó szögfelezőjének a hossza.

\begin{matrix} v = \frac{2 A' N \cdot A' R}{A' N + A' R} \cdot cos \frac{α}{2} = 2 \frac{\frac{{(b c - x y)}^{2}}{(b - y) (c - x)}}{\frac{b c - x y}{b - y} + \frac{b c - x y}{c - x}} \cdot cos \frac{α}{2} = \frac{2 (b c - x y)}{b + c - x - y} \cdot cos \frac{α}{2} . \end{matrix}

A N_{1} R_{1}

háromszögnek az

N_{1} R_{1}

oldalhoz tartozó szögfelezője pedig, mint az

A B C

háromszög

B C

oldalához tartozó szögfelezőjének

A M = v_{1}

része:

\begin{matrix} v_{1} = \frac{2 b c}{a + b + c} cos \frac{α}{2} \end{matrix}

és így

\begin{matrix} v : v_{1} = \frac{b c - x y}{b + c - x - y} : \frac{b c}{a + b + c} \end{matrix}

(2)

M T

, mint az

A B C

háromszögbe írható kör sugara:

\begin{matrix} M T = \frac{b c sin α}{a + b + c} \end{matrix}

és mint az

A C_{2} B_{2}

háromszöget kívülről érintő körnek a sugara:

\begin{matrix} M T = \frac{x y sin α}{x + y - z} \end{matrix}

és így

\begin{matrix} \frac{b c}{a + b + c} = \frac{x y}{x + y - z} \end{matrix}

(3)

a (2) aránylat tehát így alakul.

\begin{matrix} v : v_{1} = \frac{b c - x y}{b + c - x - y} : \frac{x y}{x + y - z} \end{matrix}

(4)

A (3)-ból következik,hogy

\begin{matrix} \frac{b c}{x y} = \frac{a + b + c}{x + y - z} \end{matrix}

és

\begin{matrix} \frac{b c - x y}{x y} = \frac{b + c - x - y + a + z}{x + y - z} \end{matrix}

De a

B C B_{2} C_{2}

négyszög érintő négyszög lévén:

\begin{matrix} b + c - x - y = a + z \end{matrix}

és így

\begin{matrix} \frac{b c - x y}{x y} = \frac{2 (b + c - x - y)}{x + y - z} \end{matrix}

honnan

\begin{matrix} \frac{b c - x y}{b + c - x - y} = \frac{2 x y}{x + y - z} \end{matrix}

és a (4) aránylat következőképp alakul

\begin{matrix} v : v_{1} = \frac{2 x y}{x + y - z} : \frac{x y}{x + y - z} \end{matrix}

vagyis

\begin{matrix} v = 2 v_{1} . \end{matrix}

A' N R

és

A N_{1} R_{1}

hasonló háromszögekben tehát a megfelelő szögfelezők aránya

2 : 1

, miből következik, hogy

\begin{matrix} N R : N_{1} R_{1} = 2 : 1 \end{matrix}

és

\begin{matrix} N R = 2 N_{1} R_{1} \end{matrix}

N R

és

N_{1} R_{1}

egyenesek tehát az

A' B' C'

és

A B C

hasonló háromszögekben megfelelő egyenesek; s miután a

K

és

M

pontok megfelelő egyeneseken feküsznek és összeköttetésük a hasonlósági ponton,

S

-en megy keresztül, következik, hogy:

\begin{matrix} S K : S M = 2 : 1. \end{matrix}

Látni való, hogy a

K

pont nem más, mint az

A' B' C'

háromszögbe írható kör középpontja.

(Weisz Lipót, Pécs.)

A feladatot még megoldotta: Visnya Aladár.