Kezdőlap


Feladat:	277. matematika feladat	Korcsoport: 18-	Nehézségi fok: -
Megoldó(k):	Riesz Frigyes , Strasser G. Sándor , Weisz Lipót
Füzet:	1897/február, 102 - 104. oldal		PDF \| MathML
Témakör(ök):	Ceva-tétel, Magasságpont, Körülírt kör középpontja, Szinusztétel alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1896/november: 277. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás.

1 .^{\circ}

O_{1} A B, O_{1} B C

és

O_{1} C A

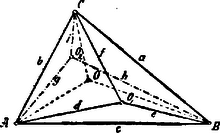
háromszögekből kapjuk, hogy

\begin{matrix} \frac{d}{e} = \frac{sin (c e)}{sin (c d)}, \frac{e}{f} = \frac{sin (a f)}{sin (a e)}, \end{matrix}

\begin{matrix} \frac{f}{d} = \frac{sin (b d)}{sin (b f)}, \end{matrix}

ezen egyenleteket egymással szorozva:

\begin{matrix} \frac{sin (a f) \cdot sin (b d) \cdot sin (c e)}{sin (a e) \cdot sin (b f) \cdot sin (c d)} = 1. \end{matrix}

(1)

Ez kriteriuma annak, hogy a három egyenes

(d, e, f)

egy pontban találkozik;

(g, h, i)

egyenesek is egy pontban metszik egymást, ha

\begin{matrix} \frac{sin (a h) \cdot sin (b i) \cdot sin (c g)}{sin (a i) \cdot sin (b g) \cdot sin (c h)} = 1. \end{matrix}

(2)

A feltételek értelmében:

\begin{matrix} (a h) = (c e), (b i) = (a f), (c g) = (b d), (a i) = (b f), (b g) = (c d), (c h) = (a e); \end{matrix}

ezeket (2)-be téve, csakugyan az (1) alatti egyenletet kapjuk.

2 .^{\circ}

(b m_{3})

és

(c m_{2})

szögek egyenlők, mert száraik egyenlők.

\begin{matrix} (b m_{3}) = (a r_{3}) és (c m_{2}) = (a r_{2}), \end{matrix}

tehát

\begin{matrix} (a r_{3}) = (a r_{2}), \end{matrix}

vagyis

B O_{2} C ▵

egyenlő szárú háromszög s így

B O_{2} = C O_{2}

. Épp így kimutathatjuk, hogy

A O_{2} = B O_{2} = C O_{2}

; ezek tehát a háromszög köré írható kör sugarai és

O_{2}

a kör középpontja.

3 .^{\circ}

\begin{matrix} (a b) + (b c) + (c a) = 180^{\circ}, \end{matrix}

(3)

\begin{matrix} (a b) = (a g) + (g b) \end{matrix}

\begin{matrix} (a g) = (a e) = (c h) és (g b) = (b f) = (c i), \end{matrix}

tehát

\begin{matrix} (a b) = (c h) + (c i) \end{matrix}

(4)

(4)-et (3)-ba téve:

\begin{matrix} (c h) + (c a) + (c i) + (b c) = 180^{\circ}, \end{matrix}

vagyis

\begin{matrix} (a h) + (b i) = 180^{\circ}; \end{matrix}

A C B O_{1}

tehát húrnégyszög s így

O_{1}

A B C

háromszög köré írható kör kerületén fekszik.

(Strasser G. Sándor, I. é. bölcsészethallgató, Budapest.)

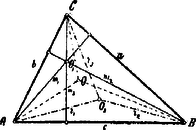
II. Megoldás.

1 .^{\circ}

Legyenek

A A''

és

A A', B B''

és

B B', C C''

és

C C'

a megfelelő szögfelezőkhöz képest symmetrikusan fekvő egyenesek; bebizonyítandó, ha a Ceva-féle tétel értelmében:

\begin{matrix} \frac{C' A}{C' B} . \frac{A' B}{A' C} . \frac{B' C}{B' A} = - 1, \end{matrix}

(1)

akkor

\begin{matrix} \frac{C'' A}{C'' B} . \frac{A'' B}{A'' C} . \frac{B'' C}{B'' A} = - 1, \end{matrix}

(2)

Kimutathatjuk, hogy

\begin{matrix} \frac{A'' B}{A'' C} . \frac{A' B}{A' C} = \frac{c^{2}}{b^{2}}, \frac{B'' C}{B'' A} . \frac{B' C}{B' A} = \frac{a^{2}}{c^{2}}, \frac{C'' A}{C'' B} . \frac{C' A}{C' B} = \frac{b^{2}}{a^{2}} . \end{matrix}

Ezen egyenleteket egymással szorozva s (1)-et tekintetbe véve, csakugyan (2)-t kapjuk.

2 .^{\circ}

A tétel második részének bebizonyítása végett elégséges kimutatnunk azt, hogy a háromszög

A A'

magassága és az

A O

egyenes (

O

a háromszög köré írható kör középpontja) symmetrikusan fekszenek a szögfelezőhöz képest. E végből nyújtsuk meg az

A O

sugarat, míg a kört

P

-ben metszi. Ekkor

A B C ∠ = A P C ∠

, mint ugyanazon íven nyugvó kerületi szögek; így tehát

90^{\circ} - A B C ∠ = 90^{\circ} - A P C ∠

, vagyis -

B A A' ∠ = P A C ∠

, a mi azt mondja, hogy

O A

és

A A'

symmetrikusan fekszenek az

A

szöget felező egyeneshez képest.

(Weisz Lipót, Pécs.)

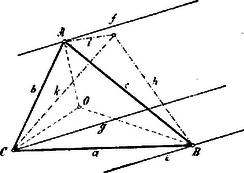
III. Megoldás.

1 .^{\circ}

A háromszög szögei

2 α, 2 β, 2 γ

. Az egyeneseknek a szögfelezőkkel képezett szögei megfelelő sorrendben

δ, ε, η

. Három egyenes

O'

pontban, másik két -

C

-ből és

B

-ből vont - egyenes

O''

pontban találkozik.

O''

-t

A

-val egybekötve,

O A O'' = φ

szöget nyerünk (a szögfelezők

O

-ban metszik egymást); a tétel első része helyes, ha

φ = δ

. Az első megoldáshoz hasonló úton találjuk, hogy

\frac{sin (α + δ)}{sin (α - δ)} = \frac{sin (α + φ)}{sin (α - φ)}

; az összegek, illetőleg külömbségek függvényeinek kifejtése és az egyenlet rendezése után kitűnik, hogy

φ = δ

(Riesz Frigyes, Győr.)

A feladatot még megoldották: Visnya Aladár, I. é. b. h., Bálint Béla, Freund Antal, Friedmann Bernát, Grünhut Béla, Hofbauer Ervin, Kántor Nándor, Klein Mór, Kornis Ödön.