Kezdőlap


Feladat:	229. matematika feladat	Korcsoport: 18-	Nehézségi fok: -
Megoldó(k):	Berger Hugó , Feuer Mór , Friedmann Bernát , Goldstein Zsigmond , Goldziher Károly , Grünhut Béla , Hofbauer Ervin , Kántor Nándor , Kornis Ödön , Riesz Frigyes , Szabó István
Füzet:	1896/december, 62 - 63. oldal		PDF \| MathML
Témakör(ök):	Ceva-tétel, Súlyvonal, Koszinusztétel alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1896/június: 229. matematika feladat

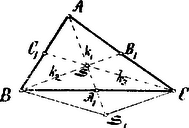
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. A Ceva-féle tétel^{$^{*}$} értelmében a középvonalak egy pontban metszik egymást, mert $A_{1} B = - A_{1} C, B_{1} C = - B_{1} A, C_{1} A = - C_{1} B$ és így:

\begin{matrix} \frac{A_{1} B}{A_{1} C} \cdot \frac{B_{1} C}{B_{1} A} \cdot \frac{C_{1} A}{C_{1} B} = {(- 1)}^{3} = - 1. \end{matrix}

2. Hosszabbítsuk meg

A A_{1} = K_{1}

középvonalat és mérjük rá

A_{1} S_{1} = A_{1} S = \frac{1}{3} K_{1}

darabot; rajzoljuk meg továbbá

S_{1} B

és

S_{1} C

segédegyeneseket; akkor

S B S_{1} C

négyszöget nyerjük, mely egyenközény, mert

S S_{1}

és

B C

átlói az

A_{1}

pontban felezik egymást; ennélfogva

S_{1} C = S B = \frac{2}{3} K_{2}

és

S_{1} B = S C = \frac{2}{3} K_{3}

S B S_{1}

és

S C S_{1}

háromszög oldalai tehát

\frac{2}{3} K_{1}, \frac{2}{3} K_{2}

és

\frac{2}{3} K_{3}

. Ezek alapján tehát a szerkesztés következőképpen történik:

S S_{1} = \frac{2}{3} K_{1}

fölé

\frac{2}{3} K_{2}

és

\frac{2}{3} K_{3}

oldalakkal megszerkesztjük az

S B S_{1}

és

S C S_{1}

háromszögeket; az így keletkezett egyenközény

B

és

C

csúcsai egyúttal a keresett háromszög két csúcsát képezik; ezután

S S_{1}

-et meghosszabbítjuk és még egyszer rámérjük

S S_{1} = S A

darabot, miáltal

A

-t, a háromszög harmadik csúcsát nyerjük.
3.

A A_{1} B

és

A A_{1} C

háromszögekből a cosinus tételt alkalmazva, nyerjük:

\begin{matrix} c^{2} = \frac{a^{2}}{4} + K_{1}^{2} - a K_{1} cos ε \end{matrix}

\begin{matrix} b^{2} = \frac{a^{2}}{4} + K_{1}^{2} + a K_{1} cos ε \end{matrix}

ε = A A_{1} B ∢

; a két egyenletet összeadva:

\begin{matrix} b^{2} + c^{2} = \frac{a^{2}}{2} + 2 K_{1}^{2}, \end{matrix}

miből

\begin{matrix} 4 K_{1}^{2} = 2 b^{2} + 2 c^{2} - a^{2} \end{matrix}

(1)

épp így

\begin{matrix} 4 K_{2}^{2} = 2 c^{2} + 2 a^{2} - b^{2} \end{matrix}

(2)

\begin{matrix} 4 K_{3}^{2} = 2 a^{2} + 2 b^{2} - c^{2} . \end{matrix}

(3)

E három egyenletet összeadva.

\begin{matrix} 4 (K_{1}^{2} + K_{2}^{2} + K_{3}^{2}) = 3 (a^{2} + b^{2} + c^{2}) \end{matrix}

(4)

(1)-ből:

\begin{matrix} b^{2} + c^{2} = \frac{4 K_{1}^{2} + a^{2}}{2} \end{matrix}

mit (4)-be téve:

\begin{matrix} 4 (K_{1}^{2} + K_{2}^{2} + K_{3}^{2}) = \frac{3}{2} (3 a^{2} + 4 K_{1}^{2}) \end{matrix}

miből

\begin{matrix} a = \frac{2}{3} \sqrt[]{2 (K_{2}^{2} + K_{3}^{2}) - K_{1}^{2}} . \end{matrix}

Épp így kapjuk, hogy:

\begin{matrix} b = \frac{2}{3} \sqrt[]{2 (K_{3}^{2} + K_{1}^{2}) - K_{2}^{2}} \end{matrix}

\begin{matrix} c = \frac{2}{3} \sqrt[]{2 (K_{1}^{2} + K_{2}^{2}) - K_{3}^{2}} . \end{matrix}

Hogy a háromszög területét kiszámíthassuk, tekintetbe vesszük, hogy

S C S_{1}

háromszög

t

területe harmadrésze az

A B C

háromszög

T

területének: de

S C S_{1}

háromszög oldalai

\frac{2}{3} K_{1}, \frac{2}{3} K_{2}, \frac{2}{3} K_{3}

, s így a területe:

\begin{matrix} t = \frac{1}{9} \sqrt[]{(K_{1} + K_{2} + K_{3}) (K_{2} + K_{3} - K_{1}) (K_{1} + K_{3} - K_{2}) (K_{1} + K_{2} - K_{3})}, \end{matrix}

ha továbbá

K_{1} + K_{2} + K_{3} = 2 K

, akkor

\begin{matrix} t = \frac{4}{9} \sqrt[]{K (K - K_{1}) (K - K_{2}) (K - K_{3})} \end{matrix}

s így

A B C

háromszög területe:

\begin{matrix} T = \frac{4}{3} \sqrt[]{K (K - K_{1}) (K - K_{2}) (K - K_{3})} . \end{matrix}

4. Legyen pl.

K_{2} = K_{3}

; ekkor

C S B

háromszög egyenlőszárú, mert

S B = S C = \frac{2}{3} K_{2} = \frac{2}{3} K_{3}

; tehát

S A_{1}

középvonal az

S C B

háromszögnek egyúttal magassága, s mint ilyen merőleges az alapra. De

S A_{1}

egybeesik

A A_{1}

-gyel, miért is

A A_{1}

középvonalból ugyancsak magasság lesz, tehát merőleges

B C

-re s így

A B C

háromszög csakugyan egyenlőszárú.

(Grünhut Béla, főreálisk. VIII. o. t. Pécs.)

A feladatot még megoldották: Berger Hugó, Feuer Mór, Friedmann Bernát,Goldstein Zsigmond, Goldziher Károly, Hofbauer Ervin, Kántor Nándor, Kornis Ödön, Riesz Frigyes, Szabó István.

^{$^{*}$}Lásd: A Ceva-féle tétel és alkalmazása; Középiskolai Mathematikai Lapok, II. évfolyam, 94. lap.