Kezdőlap


Feladat:	184. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Friedmann Bernát , Geiszt Emil , Grünhut Béla , Pósch Gyula , Szabó Gusztáv , Szabó István , Visnya Aladár
Füzet:	1896/április, 111 - 113. oldal		PDF \| MathML
Témakör(ök):	Magasságvonal, Magasságpont, Háromszögek szerkesztése, Szögfüggvények, síkgeometriai számítások, Terület, felszín, Háromszögek hasonlósága, Feladat
Hivatkozás(ok):	Feladatok: 1896/január: 184. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{\circ}$ . Ha a háromszög területe $t$ , az oldalak $a, b, c,$ akkor:

\begin{matrix} 16 t^{2} = (a + b + c) (b + c - a) (a + c - b) (a + b - c) \end{matrix}

(1)

\begin{matrix} 2 t = a m_{1} = b m_{2} = c m_{3}, \end{matrix}

miből

\begin{matrix} a = \frac{2 t}{m_{1}}, b = \frac{2 t}{m_{2}}, c = \frac{2 t}{m_{3}} \end{matrix}

(2)

Ezen értékeket

1)

-be téve, kapjuk:

\begin{matrix} 16 t^{2} = 16 t^{4} (\frac{1}{m_{1}} + \frac{1}{m_{2}} + \frac{1}{m_{3}}) (\frac{1}{m_{2}} + \frac{1}{m_{3}} - \frac{1}{m_{1}}) (\frac{1}{m_{1}} + \frac{1}{m_{3}} - \frac{1}{m_{2}}) (\frac{1}{m_{1}} + \frac{1}{m_{2}} - \frac{1}{m_{3}}) \end{matrix}

(3)

miből a háromszög területe:

\begin{matrix} t = \frac{{(m_{1} m_{2} m_{3})}^{2}}{\sqrt[]{[(m_{1} m_{2} + m_{1} m_{3} + m_{2} m_{3}) (m_{1} m_{3} + (m_{1} m_{2} - m_{2} m_{3}) (m_{2} m_{3} + m_{1} m_{2} - m_{1} m_{3}) (m_{2} m_{3} + m_{1} m_{3} - m_{1} m_{2})}} \end{matrix}

(4)

Az oldalakat a (2) alatti egyenletekből számítjuk ki.
Hogy a szögeket kiszámíthassuk, a háromszöget szétbontjuk derékszögű háromszögekre; így kapjuk:

\begin{matrix} sin α = \frac{m_{2}}{c}, sin β = \frac{m_{3}}{a}, sin γ = \frac{m_{1}}{b} \end{matrix}

(5)

vagy a (2) alatti értékeket helyettesítve:

\begin{matrix} sin α = \frac{m_{2} m_{3}}{2 t}, sin β = \frac{m_{1} m_{3}}{2 t}, sin γ = \frac{m_{1} m_{2}}{2 t} \end{matrix}

(6)

2^{\circ}

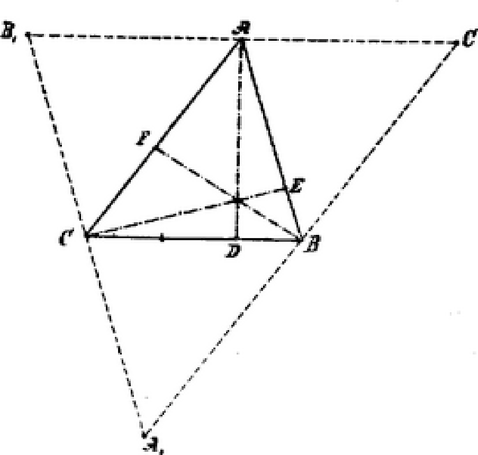
. A megadott magasságokból háromszöget szerkesztünk, melynek magasságai legyenek:

μ_{1}, μ_{2}, μ_{3}

. E magasságokból, mint oldalakból újra háromszöget szerkesztünk; ekkor:

\begin{matrix} a m_{1} = b m_{2} = c m_{3} \end{matrix}

(7)

\begin{matrix} μ_{1} m_{1} = μ_{2} m_{2} = μ_{3} m_{3} \end{matrix}

(8)

e két egyenletből kapjuk:

\begin{matrix} \frac{a}{μ_{1}} = \frac{b}{μ_{2}} = \frac{c}{μ_{3}} \end{matrix}

(9)

Ebből látjuk, hogy a

μ_{1}, μ_{2}

és

μ_{3}

-ból alakított háromszög hasonló a szerkesztendő háromszöghöz. Ennélfogva meghosszabítjuk a

μ_{1}

-hez tartozó magasságot, rámérjük

m_{1}

-et s ennek végpontján át

μ_{1}

-el párhuzamost húzunk s végre meghosszabbítjuk még a

μ_{2}

és

μ_{3}

oldalakat, míg azok a

μ_{1}

-gyel párhuzamosan rajzolt egyenest metszik.

3^{\circ}

A, B

ás

C

csúcsokon át a szemben fekvő oldalakkal párhuzamosokat húzunk, miáltal

A_{1} B_{1} C_{1}

háromszöget nyerjük.

E háromszög oldalai az

A B C

háromszög megfelelő oldalainak kétszeresei s

A, B

és

C

pontok által feleztetnek.
Mert hisz

A C B A_{1}

és

C B A C_{1}

egyenközényekben

\begin{matrix} A C = A_{1} B = B C_{1} \end{matrix}

Az eredeti háromszög magasságai tehát az

A_{1} B_{1} C_{1}

háromszög oldalainak középpontjaiban emelt merőlegesek s mint ilyenek egy pontban metszik egymást.

(Pósch Gyula, a budapesti ág. h. evang. főgymn. VIII. o. t.).

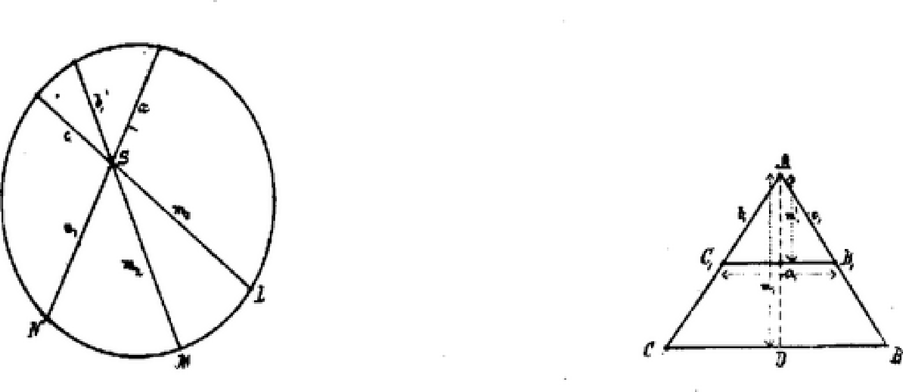
Jegyzet. A háromszög még így is szerkeszthető: Rajzolunk három, egymást egy pontban ‐

S

-ben ‐ metsző egyenest, melyekre a megadott magasságokat rámérjük. Az így nyert

L, M, N

pontokon át kört fektetünk, a magasságokat ellenkező irányban meghosszabbítjuk, mi által

a_{1}, b_{1}, c_{1}

egyeneseket nyerjük. Ezeket egy háromszög oldalainak tekintve, megrajzoljuk

A C_{1} B_{1}

háromszöget. E háromszög magasságai legyenek

m_{1}', m_{2}', m_{3}'

;

m_{1}'

-re rámérjük

m_{1}

-et, és

D

ponton át

C_{1} B_{1}

oldallal párhuzamost húzunk.

A B C

a keresett háromszög.

Meg kell mutatnunk, hogy

B

pontból rajzolt magasság egyenlő

m_{2}

-vel és a

C

pontból rajzolt magasság egyenlő

m_{3}

-mal. Miután az egymást metsző húrok metszeteinek szorzatai egyenlők, írhatjuk:

\begin{matrix} a_{1} m_{1} = b_{1} m_{2} = c_{1} m_{3}, \end{matrix}

továbbá

\begin{matrix} a_{1} m_{1}' = b_{1} m_{2}' = c_{1} m_{3}', \end{matrix}

miből

\begin{matrix} \frac{m_{1}}{m'_{1}} = \frac{m_{2}}{m'_{2}} = \frac{m_{3}}{m'_{3}} \end{matrix}

A B C

és

A B_{1} C_{1}

háromszögek hasonlók; ha tehát

m'_{1}

-et egyenlővé tesszük

m_{1}

-gyel, akkor

m'_{2}

-ből

m_{2}

és

m'_{3}

-ból

m_{3}

lesz. A feladatot megoldották: Friedmann Bernát, S.-A.-Ujhely; Szabó István, Debreczen; Geist Emil és Szabó Gusztáv, Győr; Grünhut Béla és Visnya Aladár, Pécs.