| Feladat: | 43. matematika ábrázoló geometria feladat | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Megoldó(k): | Bartók I. , Deutsch I. , Enyedi Béla , Haar A. , Hausvater József , Heimlich P. , Hirschfeld Gy. , Kertész G. , Lamparter J. , Messer P. , Pazsiczky G. , Riesz K. , Schuster Gy. | ||
| Füzet: | 1902/szeptember, 24 - 25. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Ábrázoló geometria | ||
| Hivatkozás(ok): | Feladatok: 1902/március: 43. matematika ábrázoló geometria feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Első megoldás. Ez a föladat csak akkor oldható meg, ha a keresett sík első képsíkszöge nagyobb mint az adott sík első képsíkszögének pótló szöge. Ilyenkor két megoldást kapunk; ha egyenlő vele, egyet; ha kisebb, megoldást nem kapunk. 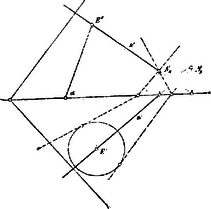 Az előbb említett háromféle eset a következően adódik ki. Ha a keresett sík képsíkszöge nagyobb, mint az adott sík képsíkszögének pótló szöge, akkor a kúp csúcsán áthaladó és az adott síkra merőlegesen álló egyenes egészen a kúpon kívül van. Az ábrában az egyenes első nyompontja a kúp alapkörén kívül fekszik. Ha a keresendő sík képsíkszöge az adott sík képsíkszögének pótló szögével egyenlő, akkor az említett egyenes a kúp alkotója; első nyompontja a kúp alapkörének kerületén van és a keresett sík a kúpot érinti. Ha végül a keresendő sík képsíkszöge az adott sík képsíkszögének pótló szögénél kisebb, akkor az egyenes a kúpon belül marad és első nyompontja a kúp alapkörén belül fekszik.
Második megoldás. Azon egyenes körkúphoz, melynek csúcsa az adott pont, alapja az első képsíkban van és alkotói az első képsíkkal oly szöget zárnak be, mint az adott szög, az adott síkra merőleges érintő síkokat illesztve, megkapjuk a keresett síkokat.
A feladatot még megoldották: Bartók J., Deutsch I., Heimlich P., Hirschfeld Gy., Haar A., Kertész G., Lamparter J., Messer P., Pazsiczky G., Riesz K., Schuster Gy. |