Feladat: 1991. évi Kürschák matematikaverseny 3. feladata Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Fleiner Balázs ,  Kálmán Tamás ,  Katz Sándor 
Füzet: 1992/február, 64 - 66. oldal  PDF  |  MathML 
Témakör(ök): Egyéb szinezési problémák, Háromszögek nevezetes tételei, Kombinatorikus geometria síkban, Kombinatorikai leszámolási problémák, Egyéb sokszögek geometriája, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1992/február: 1991. évi Kürschák matematikaverseny 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Megmutatjuk, hogy a keresett szám 1991; általában n piros pont esetén, ahol n≥3, 2n-5  kék pontra szükség lehet, többre nem.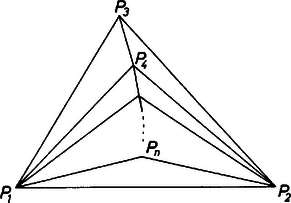

 
 

3. ábra
 
Először olyan Pi, i=1,2,...,n pontrendszert adunk meg, amelyikhez legalább 2n-5 kék pontra van szükség. Egy P1P2P3 háromszögbe rajzoljunk például egy P3-ból induló, a P1P2 oldal egy belső pontjáig menő körívet, és ennek a belsejében jelöljük ki sorra a további n-3 pontot (3. ábra.) Ekkor a P1PiPi+1, P2PiPi+1 (3≤i≤n-1) és a P1P2Pn háromszögek közül semelyik kettőnek sincs közös belső pontja, tehát mindegyik belsejében kell kék pontnak lennie. Így legalább
2(n-3)+1=2n-5
kék pontra van szükség.
Legyen most P1,P2,...,Pn tetszés szerinti piros pontrendszer. Eljárást adunk a kék pontok elhelyezésére. Választunk egy e egyenest, amelyik nem párhuzamos semelyik PiPj egyenessel, és egy elég kis d távolságot, például kisebbet az összes piroscsúcsú háromszög magasságainál. Ez lehetséges, mert csak véges sok pontpár és véges sok háromszög van.
Húzzunk most mindegyik Pi ponton át egy e-vel párhuzamos ei egyenest. Ekkor lesz olyan eu, amelyiknek az egyik oldalán nincs piros pont, és olyan ev, amelyiknek az eu-t nem tartalmazó oldalán nincsen.
Ezeken az egyeneseken nincs piros pont Pu-n, illetőleg Pv-n kívül, mert nincs három egy egyenesen levő piros pont, e választása szerint pedig ezeken az egyeneseken kettő sem lehet. Minden további ei egyenes metszi a PuPv szakaszt, ami a pontrendszer konvex burkának a belsejében halad.
Helyezzünk egy-egy kék pontot minden olyan Pi kezdőpontú félegyenesre Pi-től d távolságban, amelyiknek van közös pontja a konvex burok belsejével. Ezzel a feladat követelményeit teljesítettük. Egy piros csúcsú háromszög csúcsain át húzott egyenesek ugyanis különböznek az oldalegyenesektől. Így az egyik egyenes valamelyik félegyenesének van közös pontja a háromszög belsejével. Az ezen kijelölt kék pont d választása folytán a háromszög belsejében van.
Számoljuk össze a kék pontokat. Két-két kék pontot helyeztünk a konvex burok belsejében levő piros pontok közelébe, egyet-egyet a konvex burok határán levő piros pontokhoz, kivéve Pu és Pv-t, amikhez nem helyeztünk kék pontot. Jelöljük b-vel a konvex burok csúcsainak számát. A burok oldalszakaszainak belsejében nem lehet piros pont, így a burok belsejében n-b piros pont van. A kék pontok száma tehát
2(n-b)+b-2=2n-b-2≤2n-5.
Ezzel a bizonyítandó állítás második részét is beláttuk.
 

Megjegyzések: 1. Párhuzamos egyenesek helyett választhatunk egy O pontot a konvex burkon kívül úgy, hogy ne legyen rajta semelyik PiPj egyenesen se, és az ei=OPi egyeneseken helyezzük el a kék pontokat a fenti előírás szerint.
2. Könnyen látható, hogy az általános esetben is szükség van 2n-b-2 kék pontra. Ez következik, ha belátjuk, hogy bárhogyan is bontjuk a pontok konvex burkát olyan háromszögekre, amelyek közül semelyik kettőnek nincs közös belső pontja, a háromszögek száma mindig 2n-b-2. Ez akkor is igaz, ha lehet kettőnél több pont is egy egyenesen, csak nem mind.
Létezik a kívánt tulajdonságú felbontás. Egy ilyenhez juthatunk például úgy, hogy a pontrendszer konvex burkát háromszögekre bontjuk egy csúcsból induló átlókkal, majd veszünk egy-egy pontot, amelyik nem csúcsa megrajzolt háromszögnek, és összekötjük az őt tartalmazó háromszög vagy háromszögek csúcsaival. Véges számú pont esetén így véges számú lépésben kívánt tulajdonságú felbontáshoz jutunk.
Egy kívánt tulajdonságú felbontás háromszögeinek számát h-val jelölve ezekben a szögek összege h⋅180∘. Ezeknek a szögeknek a csúcsai pontrendszerünk pontjai. A konvex burok belsejében levő pontok mindegyike körül összesen 360∘ keletkezik (a felbontástól függetlenül). A konvex burok határán levő pontok körül keletkező szögek összege viszont egy b-szög szögeinek összege*, ami (b-2)⋅180∘. Így
h⋅180∘=(n-b)⋅360∘+(b-2)⋅180∘,   tehát   h=2n-b-2,
amint állítottuk.
* Ha egy sokszög oldalszakaszain további pontok vannak, és ezeket is csúcsoknak tekintjük egyenként 180° belső szöggel, akkor a szögek összegére vonatkozó formula nyilvánvalóan érvényben marad.