Feladat: 1991. évi Kürschák matematikaverseny 2. feladata Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Fleiner Balázs ,  Hegedűs Pál ,  Hertz István ,  Járai Antal ,  Kálmán Tamás ,  Katz Sándor ,  Kőszegi Botond ,  Poór Attila ,  Szegedi Krisztián ,  Veres Gábor 
Füzet: 1992/február, 63 - 64. oldal  PDF  |  MathML 
Témakör(ök): Térelemek és részeik, Háromszögek nevezetes tételei, Négyszögek geometriája, Háromszög alapú hasábok, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1992/február: 1991. évi Kürschák matematikaverseny 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

2. Egy konvex testnek két háromszöglapja és három négyszöglapja van. Kössük össze az egyik háromszöglap mindegyik csúcsát a vele szemközti négyszöglap átlóinak metszéspontjával. Bizonyítsuk be, hogy a három egyenes egy ponton megy át.

 

Megoldás. Meg kell határoznunk a test alakját. Egy négyszöglap éleihez csatlakozik mind a négy további lap. Mivel a test konvex, így a testet a négyszöglapok síkjai által határolt egyik konvex térrészből a háromszöglapok síkjai metszik ki.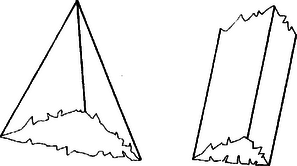
 
 

1. ábra
 

Ez a térrész egy triéder (háromoldalú testszöglet, amelyiknek a lapszögei 180∘-nál kisebbek), vagy végtelen, háromoldalú hasáb (1.ábra). Ennek a határlapjain a további két metsző sík között négyszögeknek kell keletkezniük, tehát a két sík metszésvonalának a térrészen kívül kell lennie, vagy párhuzamos a két sík. A háromszöglapoknak tehát nincs közös pontja.
Legyenek ezek a lapok A1B1C1 és  A2B2C2, a további élek pedig A1A2, B1B2, C1C2 (2. ábra). Jelöljük a B1B2C2C1, C1C2A2A1, A1A2B2B1 lapok átlóinak a metszéspontját rendre A3, B3, C3-mal, és nézzük az A1A3,B1B3,C1C3 egyeneseket.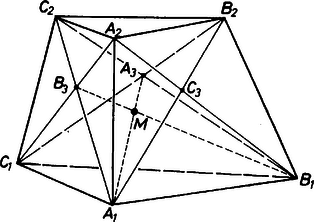
 
 

2. ábra
 

Az A1B1C2 síkmetszet B1C2 oldalának belső pontja A3,A1C2-nek pedig B3, így A1A3 és B1B3 metszi egymást a háromszög belsejének egy M pontjában. Hasonlóan látható, hogy C1C3 is metszi A1A3-at is, B1B3-at is. Az A1B1C2 síknak egyik oldalára esik C1, a másikra A2 és B2, tehát C1 és C3 is ellenkező oldalára esik. C1C3-nak tehát egy közös pontja van a síkkal, és így csak akkor metszheti A1A3-at is, B1B3-at is, ha ez a pont M. A három egyenes tehát egy ponton megy keresztül, és ezt kellett bizonyítanunk.
 

Megjegyzések: 1. A megoldást többen arra a tételre hivatkozva fejezték be, hogy ha három egyenes páronként metszi egymást, akkor vagy egy síkban vannak, vagy egy ponton mennek keresztül. Ez igaz három helyett akárhány egyenesre, és így látható be. Ha egy ponton mennek át az egyenesek, akkor igaz az állítás. Ha ez nem áll, akkor vegyünk egy P metszéspontot. Egy e egyenes, amelyik nem megy át P-n, a P-n átmenő egyeneseket (tehát legalább két egyenest) P-től különböző pontban metsz. Ekkor azonban a P-n átmenő egyenesek benne vannak a P és e által meghatározott síkban. Ebben a síkban minden további egyenes is benne van, hiszen különböző pontokban metsz legalább két P-n átmenő egyenest.
2. A feladat megoldásában valójában három metsző síkról van szó, az A1B1C2 háromszögén kívül az A1B2C1 és az A2B1C1 háromszög síkjáról. A fenti megoldás egy változatához jutunk, ha azt látjuk be, hogy A1A3,B1B3 és C1C3 ezek közül rendre két-két sík metszésvonala, és ezek nem lehetnek párhuzamosak.
3. Bár a megoldás során ismételten hivatkoztunk a test konvex voltára, ez többnyire csak bizonyos metszéspontok létrejöttének a biztosításához kellett. Felmerül a kérdés, hogy ez nem biztosítható-e egyszerűbb feltételekkel is. Ennek végiggondolását az olvasóra hagyjuk.
4. A feladat megfogalmazható síkbeli feladatként, csak azt kell figyelembe venni, hogy a test alakját vizsgálva arra jutottunk, hogy A1A2,B1B2 és C1C2 egy ponton megy keresztül, vagy párhuzamosak. A feladat tehát így szól: Az A1A2, B1B2, C1C2 egyenesek egy ponton mennek keresztül, vagy párhuzamosak. A1B2 és B1A2, B1C2 és C1B2, C1A2 és A1C2 metszéspontját sorra C3, A3, B3-mal jelölve bizonyítandó, hogy A1A3, B1B3 és C1C3 egy ponton megy keresztül, vagy párhuzamosak. (Feltesszük, hogy A3, B3 és C3 létrejön.) Bizonyításra kényelmes út az ábrát egy térbeli alakzat vetületeként felfogni. Egy síkban maradó bizonyítás igen nehéznek látszik.