Feladat: 1989. évi Kürschák matematikaverseny 3. feladata Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Balogh József ,  Benkő Dávid ,  Fleiner Tamás ,  Sebestyén Géza ,  Sustik Mátyás 
Füzet: 1990/február, 59 - 61. oldal  PDF  |  MathML 
Témakör(ök): Koordináta-geometria, Eltolás, Irracionális számok és tulajdonságaik, Egyenlőtlenségek, Abszolútértékes függvények, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1990/február: 1989. évi Kürschák matematikaverseny 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Figyeljük meg: ha az (a,b) pont nincs egyik tengelyen sem, és |a|≠|b|, akkor a négy lehetséges lépés közül háromban távolodunk az origótól, a negyedikben közeledünk hozzá.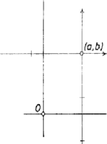

 
 

10.a ábra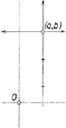
 

 
 

10.b ábra
 

Valóban, két lehetséges lépés a megfelelő koordináta abszolút értékét növeli, s mivel a másik koordinátát nem változtatja, így az origótól való távolságot is növeli. Ha a kisebb abszolút értékű koordináta abszolút értékének csökkentése irányába indulunk (10.a és 10.b) ábra), akkor már a másik koordináta egyszeresével lépve a megfelelő tengely ellenkező oldalára kerülünk, majd még növeljük az abszolút értéket a nagyobb abszolút értékű koordinátáéval, így ennek a koordinátának az abszolút értéke növekszik. A negyedik esetben a nagyobb abszolút értékű koordináta csökkentése irányában a másik egyszeresével lépve az abszolút érték csökken. Továbblépve lehet, hogy tovább csökken, de most már növekedhet is, ha a tengely ellenkező oldalára kerülünk, azonban kisebb lesz, mint a kisebb koordináta-abszolútérték volt, tehát eredeti értékéhez képest csökken. Ez esetben tehát közeledünk az origóhoz.
Jegyezzük még meg, hogy ha a koordináták aránya nem racionális, akkor továbblépés után sem válhat azzá, így egyik sem lesz 0, és egyenlőkké sem válnak. Ez teljesül a feladatban adott pontra is.
Azt bizonyítjuk be indirekt úton, hogy ha egy pont egyik koordinátája sem racionális számszorosa a másiknak, akkor abból indulva véges számú lépésben nem térhetünk oda vissza. Tegyük fel, hogy véges sok lépésben visszaérnénk. Utolsó megjegyzésünk szerint egyik pont sincs koordinátatengelyen és koordinátáik abszolút értéke különböző. Ha az első lépésben távolodunk az origótól, akkor legyen Pk az útnak az origótól legtávolabbi pontja, vagy az ilyenek egyike, és Pk-1 az út mentén előtte levő pont, Pk+1 a következő. A feltevés szerint mindkettő közelebb van az origó-hoz, mint Pk, így utóbbi ismeretében egyértelműen meg van határozva, hogy melyik pont a Pk+1. Azonban Pk-ból megengedett lépés visz Pk-1-be is, és ezzel is közeledünk az origóhoz. Így a Pk-val szomszédos pontok egybeesnek. Ez viszont nem megengedett.
Lehetséges volna még, hogy a P1-be vezető e]ső lépés közelebb vigyen az origóhoz. Ekkor P1 koordinátáinak aránya sem racionális és innen visszalépve a kiindulási pontba, majd az oda visszavezető utat fordított irányban téve meg, de csak P1-ig, olyan lépéssorozatot kapunk, amelyik ebből a pontból tér ide vissza. Ez már az origótól való távolodással indul. Ez azonban a fenti gondolatmenet szerint nem lehetséges. Semmilyen véges lépéssorozattal nem juthatunk tehát vissza kiindulási pontunkba.
 

II. megoldás. Egy u+v2 alakú számnál, ahol u és v racionális, u és v egyértelműen meg van határozva. Ha ugyanis
p+r2=s+t2,azaz(r-t)2=s-p,
akkor r=t, mert különben 2-re racionális érték adódnék, azonban 2 nem racionális; ekkor pedig p=s. Az (1,2) pontból kiindulva minden pont koordinátái u+v2 alakúak valamilyen egész u és v számmal. (Nevezzük u-t a szám egész összetevőjének.) Valóban, az (u+v2, w+z2) pontból tovább lépve világos, hogy a megváltozó koordináta újra ilyen alakú lesz.
Figyeljük meg azt is, hogy az itt szereplő egészek páros vagy páratlan volta sem változik meg, mert mindegyiket páros egésszel változtatjuk meg.
Ugyancsak világos, hogy az (u,w) és a (v,z) párok külön-külön a feladatban szereplő előírások szerint változnak, egymást nem befolyásolják.
Egy pontból kiindulva oda nem érhetünk vissza, ha mindig csak az egyik tengely irányában haladunk, az azonnali visszalépés tilalma miatt. Így az (1, 2) pontból indulva változtatni kell valamikor az ordinátát is, ha vissza akarunk jutni. Azaz a koordináták egész összetevőjének (1,0)-ról valamikor (1, 2e)-re kell változnia, ahol e vagy 1, vagy -1. Ezeket az egész összetevőket tekintve a továbbiakban koordinátáknak és a most említett lépést első lépésnek, azt mutatjuk meg teljes indukcióval, hogy a koordináták abszolút értékének a nagyobbika minden lépésben nő, és a következő lépésben a nagyobb abszolút értékű koordinátát csak úgy változtathatjuk, hogy az abszolút értéke növekedjék. Ebből következik a feladat állításának helyessége, mert ahhoz, hogy az (1,2) pontba visszajussunk, az egész összetevők maximumának 1-nek kellene lennie, de ez már az első lépés után 2 lett.
 

Az első lépésben a maximum 1-ről 2-re változott, és mivel az ordináta változott 0-ról 2e-re, ha ezt változtatjuk, a visszalépés tilalma miatt csak 4e-re változtathatjuk. Tegyük most fel, hogy a k-adik lépésben a feltételek teljesülnek. Ha a (k+1)-edik lépésben a nagyobb abszolút értékű koordinátát változtatjuk, akkor az indukciós feltevés szerint ennek abszolút értékét növelnünk kell. Ezzel a maximum is növekszik, és ha a következő lépésben is ezt a koordinátát változtatjuk, akkor csak az abszolút érték növelése irányában szabad. Ha viszont a kisebb abszolút értékű koordinátát változtatjuk, akkor a bevezetőben adott elemzésben láttuk, hogy bármelyik irányba is mozdulunk, ennek a koordinátának az abszolút értéke válik nagyobbá, és ha a következő lépést is ennek a koordinátának az irányába tesszük, akkor csak az abszolút érték növelése irányában léphetünk tovább. Ezzel állításunkat bebizonyítottuk.
 

Megjegyzés. Hasonló gondo]atmenettel bizonyítható az is, hogy az abszolút értékek minimuma nem csökkenhet.
 

III. megoldás. Az előző megoldásban abból következtettünk a feladat állításának a helyességére, hogy ha az (1, 0) pontból elindulva egyszer elmozdulunk a tengelyről, akkor a koordináták abszolút értékének a maximuma mindig nő. Ezt most indirekt úton látjuk be.
Induláskor az első koordináta páratlan, a második páros, így ez minden lépés után is így lesz, mert minden koordináta csak páros egésszel változhat. A két koordináta abszolútértéke tehát mindig különböző.
Tegyük fel, hogy valamelyik lépésben nem növekedne a koordináták abszolút értékének a maximuma. Ekkor keressük meg az első ilyen lépést. Legyen a kiinduló pont nagyobb abszolút értékű koordinátája a, a másik b. A lépés csak a változtatása, és pedig abszolút értékének csökkentése lehet, mert láttuk, hogy ha b-t változtatjuk, akkor ennek abszolút értéke |a|-nál nagyobb lesz, és ez igaz akkor is, ha a abszolút értékét növeljük.
Az előző lépésnek növelésnek kellett lennie. A visszalépés tilalma miatt ez nem történhetett az a koordináta irányában. Ha a b-2ea koordináta változott b-re, ahol e=1, vagy e=-1, ez a lépés csak úgy lehet növekedés, ha a különbség valóban kivonást jelöl. A különbség abszolút értéke ekkor 2|a|-|b|, és ez nem lehet nagyobb, mint |b|. Ebből azonban az következik, hogy |a|≦|b|, előbbi megállapításunkkal ellentétben. A koordináták abszolút értékének maximuma tehát minden lépésben növekszik.