Feladat: 1988. évi Kürschák matematikaverseny 2. feladata Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Bíró András ,  Csirik János ,  Derényi Imre ,  Fleiner Tamás ,  Kecskés Kornél ,  Keleti Tamás ,  Mándy Attila ,  Nagy Péter ,  Sustik Mátyás 
Füzet: 1989/február, 54 - 56. oldal  PDF  |  MathML 
Témakör(ök): Számhármasok, Természetes számok, Kombinatorikai leszámolási problémák, Egyenlőtlenségek, Maradékos osztás, Koordináta-geometria, Térelemek és részeik, Kocka, Tetraéderek, Téglalapok, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1989/február: 1988. évi Kürschák matematikaverseny 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. 1. Ha a középső elem egy adott b szám, akkor az első elem az 1,2,...,b-1 számok valamelyike lehet, a harmadik pedig a b+1,...,n számok valamelyike. Az előbbiek száma b-1, az utóbbiaké n-b. A kettő közül a kisebbik ‐ vagy közös értékük, ha a kettő egyenlő‐, adja meg, hogy b maximálisan hány hármasban léphet fel középső elemként.

 

Természetesen 2≦b≦n-1, és az elmondottak szerint a 2 és az n-1 egyszer, a 3 és az n-2 kétszer léphet fel maximálisan, és így tovább. Így a kiválasztható hármasok számára a következő felső korlátot nyertük: ha n páros, n=2k akkor
2⋅(1+2+...+k-1)=k(k-1)=n(n-2)/4;
ha n páratlan, n=2k+1, akkor
2⋅(1+2+...+k-1)+k=k2=((n-1)/2)2.

2. Ennyi hármas ki is választható a feltételnek megfelelő módon minden esetben. Vegyük például az {a,b,a+b} alakú hármasokat, ahol 1≦a<b és a+b≦n. Itt a hármas bármelyik két eleme meghatározza a harmadikat, így két különböző hármasnak legfeljebb egy helyen lehet egyező eleme.
Az is látható, hogy ha b≦n/2, akkor első elemnek 1-től b-1-ig minden érték előfordul, mert b-hez adva még n-nél kevesebbet ad, ha pedig b>n/2, akkor harmadik elemként b+1-től (amikor a=1) n-ig minden érték előfordul, mert a hozzájuk tartozó első elemre a=c-b<n-n/2=n/2, és ez kisebb b-nél. A kiválasztott hármasok száma tehát annyi, mint a felső korlátként kapott érték.
 

Megjegyzések: 1. A nyert eredmény írható az egészrész jelével egy formulában [((n-1)/2)2] alakban.
2. Más módokon is választhatunk ki maximális számú hármasokból álló rendszert. Ilyenek pl. az {a,a+d,n+1-d} hármasok, ahol 1≦d≦n-a2, vagy az {a,a+d,a+2d} hármasok, ahol 1≦d≦n-a2;
3. A megoldásban csak azt használtuk ki, hogy két hármas az első és második elemében, továbbá a második és harmadik elemében nem egyezhet meg. Akkor sem lehet tehát több hármast kiválasztani, ha azt megengedjük, hogy két hármas az első és harmadik elemében megegyezzék.
4. A megoldást szemléletessé tehetjük úgy, hogy a számhármasokat térbeli koordinátáknak tekintjük. Ekkor az első síknyolcadban keressük azokat az egész koordinátájú pontokat, amelyek az n élhosszúságú kockában vannak, és az a=b egyenletű átlós síknak a pozitív b-tengelyt, továbbá a b=c egyenletűnek a pozitív c-tengelyt tartalmazó oldalára esnek (a határsíkot már kizárva); végül a koordinátaegyezések kizárására vonatkozó kikötés geometriailag azt jelenti, hogy a tengelyekkel párhuzamos egyeneseken csak egy-egy kiválasztott pont lehet.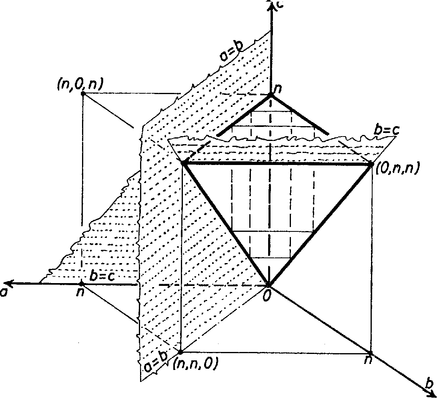
 
 
6. ábra
 

A síkok a kockából egy tetraédert vágnak ki (6. ábra). Ebből kell az utolsó feltételnek is megfelelően maximális számú pontot kiválasztani. Az egy adott b értékhez tartozó pontok a tetraéder egy téglalap alakú metszetébe eső egész koordinátájú pontok. Ezek közül nem választható ki több, mint ahány egész c értékhez tartozó, a-tengellyel párhuzamos egyenes van a téglalapon, sem annál több, mint az egész a értékhez tartozó, c tengellyel párhuzamos egyenesek száma, vagyis nem választható ki több, mint a két szám kisebbike. Ez pedig a fent nyert becsléshez vezet.
5. Többen azzal vélték megoldani a feladatot, hogy megadták a hármasoknak egy rendszerét (történetesen a föntebb említettek valamelyikét) és azt mutatták meg, hogy ezekhez nem vehető hozzá további hármas a kikötések megsértése nélkül. Ebből azonban még nem következik, hogy a kiválasztott hármasok száma maximális. Az első 5 számból válogatva pl. az {1, 2, 4}, {1, 4, 5}, {2, 3, 4} rendszer nem bővíthető, de tudjuk, hogy kiválasztható 4 hármas is úgy, hogy ne sértse meg az előírásokat.
Ezzel kapcsolatban felmerül egy probléma is. Az 1,2,...,n számok közül úgy akarunk kiválasztani a feladat feltételeinek megfelelő hármasokat, hogy további hármast már ne lehessen hozzávenni. Mi az ilyen rendszerek elemszámának a minimuma? Könnyű látni, hogy n=5-re két hármas még nem zárhat ki minden továbbit, így a kérdezett minimum 3. Az előző megjegyzésben leírt szemléltetés segítségével sikerült n=6, 7, 8, 9-re rendre 5, 7, 10, illetőleg 13 hármasból álló, nem bővíthető rendszert találni, de lehet, hogy ezek nem a minimális értékek. (A kiválasztható hármasok maximális száma ezekre az n értékekre 6, 9, 12, illetőleg 16.)
Ha a feltételt a 3. megjegyzésben említett gyengébbel helyettesítjük, akkor már igaz, hogy a hármasok minden olyan rendszere, amelyik nem bővíthető, maximális elemszámú. Valóban, két különböző középsőelemű hármas nem zárja ki egymást, ha pedig azok közt, amelyek középső eleme ugyanaz a b érték, és nem fordul elő b≦n2 esetén valamilyen a<b érték első elemként, illetőleg b>n/2 esetén valamilyen b+1 és n közti c érték harmadik elemként, akkor van olyan {a,b,c} hármas, amelyik hozzávehető a rendszerhez, mert az előbbi esetben a harmadik helyre, az utóbbiban az első helyre legalább annyi szám áll rendelkezésre, mint a másik helyre.