Feladat: 1988. évi Kürschák matematikaverseny 1. feladata Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Bíró András ,  Csirik János ,  Derényi Imre ,  Fleiner Tamás ,  Hausel Tamás ,  Kecskés Kornél ,  Keleti Tamás ,  Mándy Attila ,  Nagy Péter ,  Pásztor Gábor ,  Sustik Mátyás 
Füzet: 1989/február, 50 - 54. oldal  PDF  |  MathML 
Témakör(ök): Négyszögek geometriája, Háromszögek nevezetes tételei, Egyéb sokszögek geometriája, Paralelogrammák, Középpontos tükrözés, Eltolás, Magasságvonal, Mértani helyek, Síkgeometriai számítások trigonometriával, Trigonometriai azonosságok, Trigonometrikus függvények, Vektorok vektoriális szorzata, Vektorok lineáris kombinációi, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1989/február: 1988. évi Kürschák matematikaverseny 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Azt mutatjuk meg, hogy ha van a feladatban leírt tulajdonságú P pont, akkor az az egyik átlón van (az átló felezőpontja). Ebből következik a feladat állítása, mert ha P például a BD átlón van, akkor a BCD háromszög a PBC és a PCD háromszög egyesítése. A részháromszögek területe a négyszög területének negyedrésze, így a BD átló két egyenlő területű részre osztja a négyszöget.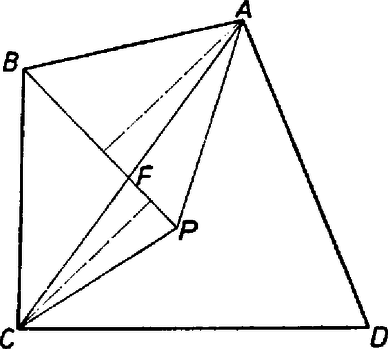
A továbbiakban egy KL...V sokszög területét τKL...V-vel fogjuk jelölni.

 
 
1. ábra
 

Mivel τABP és τBPC egyenlő, és a két háromszög BP oldala közös, így a rá merőleges magasságok is egyenlők. A és C tehát egyenlő távol van a BP egyenestől, annak két oldalán (1. ábra). Ebből következik, hogy az egyenes átmegy az AC átló F felezőpontján. Ugyanígy nyerjük, hogy DP is átmegy F-en. Ha a két egyenes különböző, akkor csak egy metszéspontjuk van, így P azonos F-fel, vagyis P az AC átlón van. Ha viszont a két egyenes egybeesik, akkor ez az egyenes a BD átló egyenese, tehát ekkor P a BD átlón van. Ezzel a feladatot megoldottuk.
 

Megjegyzések. 1. Nyilvánvalóan igaz a feladat állításának a megfordítása: Ha valamelyik átló felezi a négyszög területét, akkor van olyan P pont a négyszög belsejében, amelyikre
τABP=τBCP=τCDP=τDAP.
Nyilván ilyen pont a területet felező átló felezőpontja.
2. Az utolsó mondatban mondhattuk volna: "ez a pont ...'', mert legfeljebb egy ilyen pont lehet a négyszög belsejében. Ha ugyanis a P pontra a 4 háromszög területe egyenlő és egy P' pont pl. az ABP háromszög P-től különböző pontja, akkor
τABP'<τABP,
így P'-re nem teljesülhetnek a megfelelő egyenlőségek.
3. Lényeges az a kikötés, hogy a P pont a négyszög belsejében legyen, ugyanis létezhet a négyszögön kívül is olyan pont, amelyikre a négy háromszög területe ugyanakkora. Induljunk ki egy APBR paralelogrammából. A BR oldalon válasszunk ki egy S pontot R-hez közelebb, mint B-hez. Legyen C a PS és AR egyenes metszéspontja, D pedig B-nek az S-re vonatkozó tükörképe (2. ábra).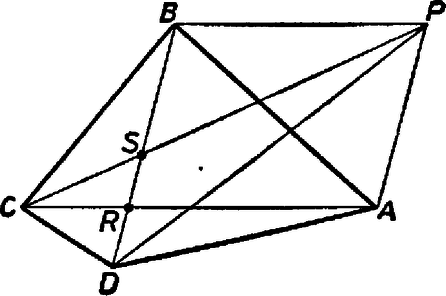
 
 
2. ábra
 

S választása folytán C az AR szakasz R-en túli meghosszabbításán van, D pedig BR-nek az R-en túli meghosszabbításán, tehát az ABCD négyszög konvex. Ekkor könnyen látható, hogy a PDA, PAB, PBC, PCD háromszögek területe egyenlő, viszont P nincs rajta egyik átlón sem.
Belátható, hogy minden ellenpélda ilyen felépítésű, annak alapján, hogy ha két háromszög területe egyenlő és egy oldaluk közös, akkor a közös oldal egyenese vagy felezi a harmadik csúcsokat összekötő szakaszt, vagy párhuzamos vele.
 

II. megoldás: Paralelogrammák esetén egyrészt az átlók metszéspontja megfelel P pontnak, másrészt mind a két átló felezi a négyszög területét, tehát a feladat állítása igaz. A továbbiakban paralelogrammáktól különböző négyszögekre szorítkozunk. Tegyük fel, hogy AB és CD nem párhuzamos.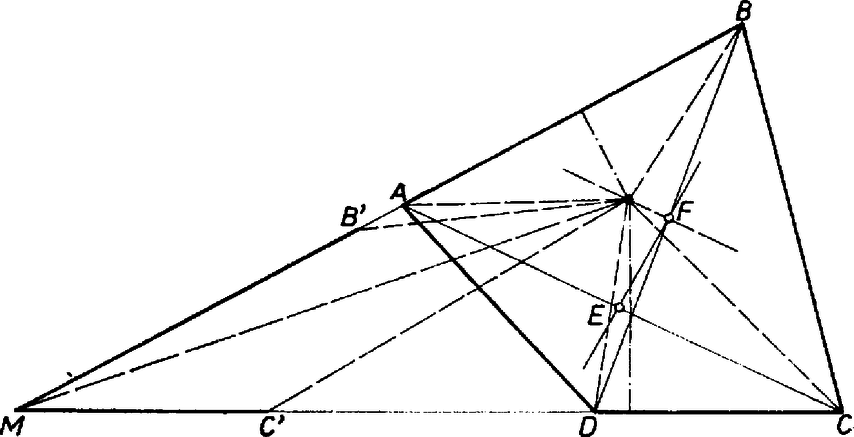
 
 
3. ábra
 

Ha egy P pontra teljesülnek a feladat feltételei, akkor az ABCP négyszög területe az adott négyszög területének a fele. Az olyan P pontok, amelyektől csak ennek teljesülését kívánjuk meg, egy AC-vel párhuzamos egyenesen vannak, mert az ABC háromszög területe nem függ a P pont helyzetétől, így az ACP háromszög területének is egy megadott értéknek kell lennie (3. ábra). Ez az egyenes lehet AC bármelyik oldalán, vagy lehet az átló egyenese is. A BD átlót ez az egyenes az F felezőpontjában metszi, mert
τABF=12τABDésτBCF=12τBCD,
a jobb oldalon szereplő háromszögek pedig együtt az adott négyszöget adják.
A feladat feltételeit kielégítő P pontra az ABP és CDP háromszögek területének az összege is az adott négyszög területének a felét adja. Az ezt a feltételt kielégítő P pontok is egy egyenesen sorakoznak. Feltettük, hogy az AB és a CD egyenes nem párhuzamos. Jelöljük metszéspontjukat M-mel és a betűzést válasszuk úgy, hogy ez az oldal A-n, illetőleg D-n túli meghosszabbítására essék. Toljuk el ezután az oldalakat egyenesük mentén úgy, hogy A, illetőleg D az M pontba kerüljön. A keletkező MB', illetőleg MC' oldalakra P-ből húzott magasság nem változott meg, így az MB'C'P négyszög területe is az eredeti négyszög területének a fele, a keresett pontok tehát egy B'C'-vel párhuzamos egyenesen vannak, amint azt az előzőekben beláttuk.
Ez az egyenes átmegy az átlók felezőpontján, ugyanis a CDF háromszög területe is a BCD háromszög területének a fele, így az ABF és a CDF háromszög együttes területe az ABCD négyszög területének a fele. Ugyanígy belátható, hogy az AC átló E felezőpontja is a szóban forgó egyenesen van. A P pont ezek szerint az EF egyenesnek és az F ponton át AC-vel párhuzamosan húzott egyenesnek a metszéspontja, vagyis F, ha a két egyenes különbözik. Ez esetben a BD átló felezi az ABCD négyszög területét.* A két egyenes akkor esik egybe, ha az elsőnek említett egybeesik az AC egyenessel. Ekkor viszont P az AC átlón van, s így ez az átló felezi a négyszög területét.
 

Megjegyzések: 1. A megoldásban két mértani hely szerepelt, amelyek a következő alakban egyesíthetők: Adott a síkban két szakasz, keressük azoknak a pontoknak a mértani helyét, amelyeket a két szakasz végpontjaival összekötve a keletkező két háromszög területének az összege egy adott érték. A feladat megoldásához nem volt szükség a mértani hely pontos meghatározására.
A feladat megoldása során azt is láttuk, hogy ha a két szakasz nem párhuzamos, akkor az általánosság megszorítása nélkül feltehető, hogy egyik végpontjuk közös. Ez esetben a két szakasz egy-egy félegyenest határoz meg, és a mértani helynek a köztük levő szögtartományba eső részét egy, a másik végpontokat összekötő egyenessel párhuzamos egyenes tartalmazza. Könnyű látni, hogy a mértani helynek a szögtartományba eső része az egyenes ideeső szakasza, és az egész mértani hely annak a paralelogrammának a határa, amelyiknek ez a szakasz az egyik oldala és középpontja a szakaszok közös végpontja.
Egyszerűsödik a helyzet, ha a területeket előjeles mennyiségeknek tekintjük a következő módon: megadjuk a határnak a körüljárási irányát (sokszögeknél pl. az egymás utáni csúcsok felsorolásával), és pozitívnak tekintjük a területet, ha a körüljárási irány az óramutató járásával ellentétes, negatívnak, ha azzal megegyező.
Könnyen látható, hogy ez esetben nem változik a mértanihely-problémában a területösszeg akkor sem, ha az egyenes mentén kilépünk a szögtartományból, s így a mértani hely egy egyenes lesz.
Bonyolódik a helyzet, ha a két szakasz párhuzamos. Ha pl. a területet mindig pozitív mennyiségnek tekintjük és a két szakasz egyenlő hosszú, továbbá a két háromszög területének összege a szakaszok meghatározta paralelogramma területének a fele, akkor a két szakasz egyenesei közti sáv összes pontja alkotja a mértani helyet. A területösszeg nem lehet kisebb ennél az értéknél.
A kérdés további elemzését az Olvasóra bízzuk.
 
 
4. ábra
 

III. megoldás. Jelöljük a P pontból a négyszög csúcsaihoz vezető szakaszokat és a köztük levő szögeket a, b, c, d-vel, illetőleg α, β, γ, δ-val amint a 4. ábra mutatja, és írjuk fel a feladatban szereplő négy háromszög kétszeres területének az egyenlőségét, a területet két oldallal és a köztük levő szöggel fejezve ki:
absinα=bcsinβ=cdsinγ=dasinδ.
Innen az első és a harmadik kifejezés szorzata egyenlő a második és a negyedik szorzatával. A 0-tól különböző abcd szorzatot mindkettőből elhagyhatjuk és a következő, szögek közti összefüggést kapjuk:
sinαsinγ=sinβsinδ.
Az összefüggést a
2sinφsinψ=cos(φ-ψ)-cos(φ+ψ)
azonosság alapján így alakíthatjuk át:
cos(α-γ)-cos(α+γ)=cos(β-δ)-cos(β+δ).

Tudjuk azt is, hogy a négy szög összege 360∘, ezért
cos(β+δ)=cos(-(α+γ))=cos(α+γ),
és így a két kisebbítendő is egyenlő. Az egyes szögek 180∘-nál kisebb pozitív szögek, így a szögkülönbségek -180∘ és 180∘ közt vannak. Koszinuszaik tehát csak úgy lehetnek egyenlők, ha a szögek vagy egyenlők, vagy egymás ellentettjei. Az első esetben
α-γ=β-δazazα+δ=β+γ,
és mivel a négy szög összege 360∘, így az egyenlőség mindkét oldalán 180∘ áll, azaz P a BD szakaszon van, tehát BD felezi a négyszög területét.
A második esetben
α-γ=δ-βazazα+β=γ+δ.
Ekkor P az AC átlón van, és ez felezi a négyszög területét.
 

IV. megoldás. Megoldhatjuk a feladatot a vektoriális szorzat felhasználásával is. Jelöljük a P pontból a csúcsokhoz mutató vektorokat a, b, c, d-vel. Ekkor a feltételben szereplő négy háromszög területének egyenlőségét az
a×b=b×c=  c×d=d×a  
egyenlőségek fejezik ki. Valóban, az egyes vektorszorzatok hossza a háromszögek területének a kétszerese, és a vektorok a sík ugyanazon oldalára mutatnak, mert a P pont a négyszög belsejében van.
Képezzük az első és második, továbbá a harmadik és negyedik szorzat különbségét és használjuk fel, hogy a vektoriális szorzat a tényezők felcserélésével az ellentettjére változik, továbbá a disztributív tulajdonságát:
o=a×b-b×c=a×b+c×b=(a+c)×b;  
és hasonlóan kapjuk, hogy
o=(c+a)×d.  
Az először nyert szorzat csak úgy lehet a nullavektor, ha a+c =o, vagy a+c és b párhuzamos. Az első esetben c=-a, ami azt jelenti, hogy P az AC átló felezőpontja, így ez az átló felezi a négyszög területét. Ha viszont a+c nem o és párhuzamos b-vel, akkor a második nyert összefüggésből adódik, hogy d-vel is párhuzamos, vagyis b és d párhuzamos vektorok. Ekkor tehát P a BD átlón van, és így ez az átló felezi a négyszög területét.
 
Megjegyzés. Az adott négyszög konvex voltát csak annyiban használtuk fel, hogy a megoldásban szereplő vektoriális szorzatok a sík ugyanazon oldalára mutatnak. Ez azonban konkáv négyszögre is teljesül, ha a P-ből a csúcsokhoz húzott szakaszok a négyszög belsejében vannak.
Belátjuk, hogy ha konkáv négyszög belsejében van a feltételnek eleget tevő 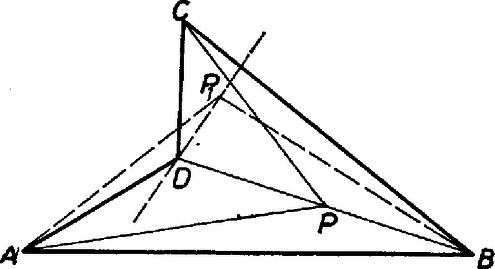P pont, akkor az utoljára mondott feltétel teljesül rá, és így a feladat állítása a konvexitás kikötése nélkül is igaz. Valóban, ha a négyszög konkáv szöge a D csúcsnál van, akkor a τADP=τCDP egyenlőségből következik, hogy a DP egyenes vagy felezi az AC szakaszt, vagy párhuzamos vele. Az első esetben a PA, PB, PC, PD szakaszok a négyszög belsejében futnak. Ha viszont egy P1 pontra az utóbbi teljesül, akkor vagy az ABP1 háromszög, vagy a BCP1 háromszög tartalmazza a D pontot (5. ábra), mondjuk, az előbbi eset áll fenn. Ekkor a háromszög tartalmazza az ADP1 háromszöget is, tehát területe nagyobb, mint az utóbbié, így nem teljesülhet a P1 pontra a feladat feltétele.
 
 
5. ábra
 
*Ábránk esetében nincs a feltételt kielégítő P pont, sem a négyszög területét felező átlő, annak érdekében, hogy a két mértani hely különváljék.