Feladat: 1984. évi Kürschák matematikaverseny 3. feladata Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Csizmadia György ,  Erdős László ,  Szabó Zoltán 
Füzet: 1985/február, 59 - 61. oldal  PDF  |  MathML 
Témakör(ök): Természetes számok, Számhalmazok, Teljes indukció módszere, Oszthatóság, Kombinatorikai leszámolási problémák, Kombinatorika, Függvények, Különleges függvények, Függvény határértéke, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1985/február: 1984. évi Kürschák matematikaverseny 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jegyezzük meg először, hogy a számhalmaz legkisebb eleme az eljárás folyamán nem nőhet, a legnagyobb pedig nem csökkenhet. Valóban, a legkisebb elem csak úgy változhat, vagy ha többször szerepel és ezek közül kettőt megváltoztatunk, vagy egy nála nagyobb, többször szereplő szám megváltoztatása során a kisebbített szám átlépi. Mindkét esetben keletkezik egy nála kisebb szám. Hasonló meggondolás érvényes a legnagyobb elemre is.
Vizsgáljuk a legközelebbi egészek közti távolságok változását az eljárás során. Ha egy kétszer szereplő n számot (n-q)-val és (n+p)-vet helyettesítünk, akkor a köztük levő 0 hosszúságú intervallum megszűnik és keletkezik (n-q)-tól a megelőző adott számig, ha van ilyen, egy korábbi intervallumnál nem hosszabb köz: (n-q)-tól a rákövetkezőig egy legfeljebb p+q hosszúságú; (n+p)-től a megelőzőig, ha ez nem n-q, és (n+p)-től a rákövetkezőig, ha van ilyen, egy-egy valamilyen korábbinál nem hosszabb intervallum.
Azt kaptuk tehát, hogy egész számaink közül a szomszédosak közti távolság sohasem nagyobb, mint p+q, vagy valamelyik kezdetbeni távolság.
Ezeket tudva a feladat állítását teljes indukcióval bizonyítjuk. Nyilvánvalóan igaz az állítás, ha 1 vagy 2 egész szám van adva. Tegyük fel, hogy igaz az állítás, ha k darab egész szám adott, és tekintsünk egy k+1 egész számból álló rendszert. A számokat nagyság szerint rendezve, a szomszédosak közti k számú távolság egyike sem nagyobb, semelyik lépés után sem, mint az eredetileg adott számok közti távolságok és p+q közt fellépő legnagyobb érték. Ezt d-vel jelölve a legkisebb és legnagyobb szám közti távolság eszerint nem lépheti túl a kd értéket. Mivel a legkisebb szám nem nő, a legnagyobb nem csökken és egész számokról van szó, ez csak úgy lehetséges, ha bizonyos számú lépés után a legnagyobb szám már nem változik (a legkisebb sem). Innen kezdve azonban elegendő a legnagyobb szám elhagyásával maradó k számot vizsgálni, ezek közt pedig indukciós feltevésünk szerint véges számú lépésben befejeződik az eljárás. Ez a tulajdonság tehát átöröklődik a k+1 egészből álló rendszerre is. Ezzel a bizonyítást befejeztük.

 

II. megoldás. Ismét használjuk az I. megoldásnak azt a megállapítását, hogy a legkisebb elem nem nő, a legnagyobb nem csökken. Megmutatjuk ezen kívül, hogy ha kerülnek is esetleg számok a változtatás során az eredeti számokat tartalmazó számközön kívül, a számköz hossza nem nőhet n(p+q)-nál többel. Ehhez figyeljük meg, hogy ha a c, c+p+q számközben, a határokat is beleértve, van valamelyik lépés után egy az n szám közül, mondjuk d:
c≤d≤c+p+q,
akkor d esetleges megváltoztatása esetén vagy d-q≥c és erre c≤d-q≤c+p+q, vagy ha d-q<c, akkor
d+p=d-q+p+q<c+p+q,
s így erre teljesül a fenti kettős egyenlőtlenség. Így a továbbiak során is mindig lesz legalább egy a számaink közül a c, c+p+q számközben.
Ha az eljárás során egy szám az eredeti számokat tartalmazó számközön kívül kerül, akkor attól legfeljebb p, ill. q távolságra kerülhet, tehát az első p+q hosszúságú intervallumon nem jut túl. Így ha mind az n egész szám kívül kerül is az eredetileg adott számokat tartalmazó számközön (pl. ha eredetileg az összes számok egyenlők voltak), akkor is le- és fölfelé összesen n darab p+q hosszúságú intervallum már biztosan tartalmazni fogja minden lépés után az összes számot.
Hozzárendelünk harmadrészt szám-n-esünkhöz egy olyan függvényt, amelyik minden határon túl nő, ha az eljárás nem fejeződik be, de ezt csak úgy érheti el, ha a számokat tartalmazó számköz is minden határon túl nő. Mivel láttuk, hogy ez nem lehetséges, ezzel bizonyítást nyer állításunk.
Ha p≠q, feltehetjük, hogy p>q, mert ellenkező esetben minden számot az ellentettjével helyettesítve az egyenlők egyikét q-val növelni, a másikat p-vel csökkenteni kell. Legyen a függvényünk ebben az esetben a számok összege. Ez minden lépésben (p-q)-val nő, tehát tetszés szerint nagy lesz, ha megfelelő sokszor ismételjük az eljárást. Ez azonban csak úgy következhetnék be, ha a legnagyobb szám is minden határon túl nőne. A legkisebb viszont nem nőhet, tehát a számainkat tartalmazó számköznek is minden határon túl kellene nőnie, és láttuk, hogy ez nem lehetséges.
Ha p=q, akkor vegyük a számaink közt levő n(n-1)/2 távolság összegét. Két egyenlő számot megváltoztatva csak ezeknek a többiektől való távolsága változik. Egymástól való távolságuk 0-ról 2p-re nő. Ezenkívül, ha az egyenlő számok értéke b, és egy c szám legalább p távolságra van b-től, akkor a változtatás után az egyik számtól való távolság p-vel csökken, a másiktól p-vel nő, összegük tehát nem változik. Ha viszont c a b-től p-nél kisebb távolságra van, akkor a 2|b-c| távolság 2p-re nő (14. ábra). A tekintett összeg tehát minden lépésnél legalább 2p-vel nő. Ez az összeg is csak úgy nőhetne minden határon túl, ha a legkisebb és legnagyobb szám közti távolság is minden határon túl nőne, ez pedig nem lehetséges, mint láttuk. Ezzel a feladat állításának bizonyítását befejeztük.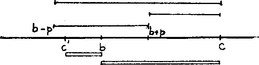
 
 
14. ábra
 

Megjegyzések. 1. Egy versenyző szellemes ötlettel rekurzív eljárást adott meg minden n-re olyan korlát meghatározására, aminél messzebb egyetlen szám sem juthat az eredeti számokat tartalmazó intervallumtól. Eljárása azonban bonyolultabb a fentinél és rosszabb korlátot is eredményez.
 

2. Az I. megoldásban egy lépésnél hivatkoztunk arra, hogy egész számokról van szó, a II. megoldásból azonban látható, hogy ennek semmi szerepe nincs az állítás helyességében. A megadott függvény mindkét esetben minden határon túl nő, akár egész számokról van szó, akár nem. A feladat állítása tehát igaz, bármilyen n valós szám van adva és bármilyen pozitív szám is p és q.
 

3. Volt versenyző, aki azt állította, hogy a végül keletkező szám-n-es ugyanaz lesz, akármilyen sorrendben végezzük el az egyenlő párok megváltoztatását, vagy eleve egy általa meghatározott sorrend esetében próbált bizonyítani. Az állítás helyes volta belátható, ha már tudjuk, hogy a feladat állítása igaz. Annak bizonyításához azonban így sem használható fel.
 

Azt fogjuk bebizonyítani teljes indukcióval, hogy bármilyen sorrendben végezzük is az egyenlő párok megváltoztatását, a végeredmény is, a végzett lépések száma is ugyanaz lesz, mintha először sorra az összes, kezdetben egyenlő számokat változtatjuk meg, majd az ezen változtatások során keletkező összes egyenlő párokat, és így tovább.
 

Ha van 0 lépésből álló eljárás, ez azt jelenti, hogy csupa különböző szám van adva, tehát más eljárás nem lehetséges, az állítás ebben az esetben igaz. (Ugyanígy egyértelmű az eljárás, és így a végeredmény is, ha van egyetlen lépésben befejeződő eljárás.)
 

Tegyük fel, hogy igaz a bizonyítandó állítás minden olyan számegyüttes esetére, amelyhez van k-nál kevesebb lépésben befejeződő lépéssorozat. Tekintsünk egy olyan számegyüttest, amelyiknél van egy, k lépésben befejeződő eljárás (k>0). Ha az eljárás azzal kezdődik, hogy először az összes, kezdetben egyenlő párokat változtatjuk meg, akkor a maradó, k-nál kevesebb lépésből álló eljárást helyettesíthetjük azzal az eljárással, amelyben először az összes meglevő, egyenlő számokból álló párt megváltoztatjuk, majd az összes így keletkezett egyenlő párokat és így tovább. Feltevés szerint ezzel a végeredmény nem változik, a lépésszám sem, tehát ugyanez igaz az eredeti eljárásra is.
 

Ha valamelyik, kezdetben meglevő, egyenlő számokból álló pár megváltoztatása előtt újonnan keletkezett párokat is változtat az eljárás, akkor menjünk el csak addig a lépésig, amelyikben a kérdéses párt változtatjuk meg. Ennek sorra kell kerülnie, mert az eljárás akkor fejeződik be, amikor az összes szám különböző (és tudjuk, hogy ez bekövetkezik). Változtassuk meg először a kérdéses párt, és utána végezzük el az ezen pár megváltoztatása előtti lépéseket. Ezzel az eljárás kérdéses részének az eredményét sem változtattuk meg, a lépések számát sem. Ha még maradt kezdetben egyenlő pár, amit csak újonnan keletkezett párok változtatása után változtattunk meg, azokra alkalmazzuk a leírt változtatást. Így véges számú lépésben az első esetre jutunk vissza anélkül, hogy közben akár az eljárás végeredményén, akár a lépésszámon változtatnánk.
 

Ezzel beláttuk, hogy az állítás helyessége öröklődik a k-nál kevesebb lépésből álló eljárásokról a k lépésből állókra, s így a bizonyítást befejeztük.
 

4. A feladattal kapcsolatban felmerül néhány probléma, amelyeknek a tisztázása talán nem lesz túlságosan nehéz. Adott n, p és q esetén maximálisan mennyivel növekedhet meg a számokat tartalmazó számköz hossza? Mi a lépések számának a maximuma? Igaz-e, hogy mindkettő akkor lesz a legnagyobb, ha p=q és az összes számok egyenlők, illetőleg páratlan n esetén egynek az értéke p-vel tér el a többiétől?