Feladat: 1984. évi Kürschák matematikaverseny 2. feladata Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Birkás György ,  Csillag Péter ,  Erdős László ,  Kós Géza ,  Oláh András ,  Pál Gábor ,  Szabó Zoltán 
Füzet: 1985/február, 55 - 58. oldal  PDF  |  MathML 
Témakör(ök): Geometria határterületei, Egyenlő szárú háromszögek geometriája, Szabályos sokszögek geometriája, Háromszög-rácsok geometriája, Hatszög-rácsok geometriája, Tengelyes tükrözés, Középvonal, Térgeometria alapjai, Vektorok, Vektorok lineáris kombinációi, Egyéb szinezési problémák, Oszthatóság, Möbius-szalag, Rombuszok, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1985/február: 1984. évi Kürschák matematikaverseny 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Ha a feladatban leírt felület síkba hajtogatható, pl. az A1A2B1 háromszög síkjába, akkor a többi háromszög ezt a háromszöget tartalmazó háromszögrács egy-egy háromszögét fogja fedni. Ha a hajtogatás sikerült, akkor vágjuk fel az összehajtogatott felületet az A1B1 él mentén és hajtogassunk tovább, amíg az összes többszörös fedést meg nem szüntetjük. Így egy paralelogrammához jutunk. Ez utóbbi hajtogatások a síknak a rács egy-egy egyenesére való tükrözésével valósíthatók meg. Rajzoljuk meg azt a két szabályos hatszöget, amelyiknek egyik oldala A1B1 és az ehhez csatlakozó hatszögrácsot a síkban (4. ábra).

 
 
4. ábra
 

Figyeljük meg, hogy bármelyik tükrözésnél ez a hatszögrács önmagába megy át, tehát a kiterítés után az A1B1 él másodszori képe is hatszögoldalra, sőt párhuzamos hatszögoldalra kellene hogy kerüljön. A sávba eső párhuzamos hatszögoldalak közt azonban 6-6 szabályos háromszög van, 28 pedig nem osztható 6-tal, tehát a keletkező felület nem lehet síkba hajtogatható.
 

II. megoldás. Az egyes háromszögek AiAi+1, ill. BiBi+1 oldallal párhuzamos középvonalai zárt törtvonalat alkotnak a térben. Síkba hajtogatva ezek továbbra is zárt törtvonalat alkotnak, tehát mint vektoroknak ‐ alkalmasan irányítva ‐ az összegük a nulla-vektor. Két egymás utáni vektornak az iránya vagy megegyezik, vagy, ha a köztük levő él mentén hajtogatás történt, egyik vagy másik irányban 120∘-ot zárnak be egymással (5. ábra).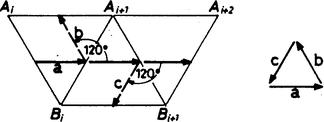
 
 
5. ábra
 

A zárt törtvonal egyes szakaszai tehát az egymással 120∘-ot bezáró és egyenlő hosszú a, b vagy c vektorral egyenlők. Legyen r az a vektorok száma, s a b-ké, t a c-ké, akkor tudjuk, hogy
a+b+c=0,ra+sb+tc=0,r+s+t=28.

Az első két egyenletből pl. c-t kiküszöbölve és átrendezve az
(r-t)a=(t-s)b
egyenlethez jutunk. Mivel a és b nem párhuzamos, ez csak úgy lehet, hogy
r-t=t-s=0,azazr=s=t,s így3r=28


a harmadik egyenletből. Ez azonban nem lehet, mert r' egész szám. A felület tehát nem hajtogatható egy síkba.
 

III. megoldás. Ha a feladatban szereplő felület síkba hajtogatható, akkor síkba kiterített hálója is (6. ábra) összehajtogatható úgy, hogy a két A1, ill. B1 pont egymásra kerüljön.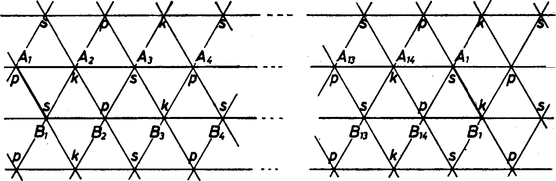
 
 
6. ábra
 

Minden hajtásnál a háló háromszögei a hálót tartalmazó háromszögrács egy-egy háromszögébe mennek át. Színezzük az A1, B1, A2 csúcsokat sorra pirosra, sárgára és kékre. Ekkor folytathatjuk a színezést a három színnel úgy, hogy az egész háló és az egész azt tartalmazó síksáv háromszögeinek a csúcsai különböző színűek legyenek. Az A1, A2, ... pontok sorozata periodikusan ismétlődve piros, kék, sárga színű lesz, a B1, B2, ... pontok pedig sárga, piros, kék színűek. Ezután tükrözve az A-k, ill. B-k egyenesére, majd sorra a keletkező újabb határvonalakra az egész háromszögrács összes csúcsainak olyan színezését kapjuk három színnel, amelynél minden háromszög csúcsai különböző színűek. Ha most a rács bármelyik egyenesére tükrözünk, minden csúcs ugyanolyan színű csúcsba megy át. Ahhoz tehát, hogy a kívánt hajtogatás lehetséges legyen, a két A1-gyel jelzett csúcsnak egyszínűnek kellene lennie, azonban az egyik piros, a másik sárga. A kívánt hajtogatás tehát nem lehetséges.
 

IV. megoldás. Vizsgáljuk az A1B1A2B2A3...A14B14A1 zárt törtvonalat. Ennek két-két szomszédos szakasza mindig egy háromszöglap két éle, tehát 60∘-ot zár be. A felület háromszögei a sík egy szabályos háromszögrácsának a háromszögeibe kerülhetnek csak.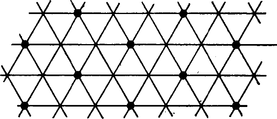
 
 
7. ábra
 

Jelöljünk meg egy csúcsot, ahová A1 kerül (7. ábra). Ekkor B1 annak a szabályos hatszögnek egyik csúcsába kerül, amelyiknek a megjelölt csúcs a középpontja, A2 pedig valamelyik szomszédos csúcsába, mert a szomszédos szakaszok 60∘-ot zárnak be. B2 ezután vagy újra a megjelölt csúcsba kerül, vagy annak a hatszög valamelyik oldalára vonatkozó tükörképébe. Jelöljük meg ezeket is. Az eljárás most már ismételhető. A következő két pont ismét egy megjelölt pont körüli szabályos hatszög két szomszédos csúcsába kerül, a harmadik vagy egy már megjelölt pontba kerül, vagy egy ilyennek a körülötte levő hatszög valamelyik oldalára vonatkozó tükörképébe. Jelöljük meg ezeket is. Ilyen módon minden harmadik szakasz végpontja kerül megjelölt pontba, tehát pl. a 27. szakasz végpontja. Ekkor azonban a 28. szakasz végpontja nem kerülhet A1-be. A kívánt hajtogatás tehát nem lehetséges.
 

Megjegyzések. 1. Láttuk, hogy ahhoz, hogy, a keletkező felület síkba hajtogatható legyen, a háromszögek számának oszthatónak kell lennie 6-tal. Többen állították, hogy ez elegendő is. Ez így már csak azért sem igaz, mert a 6 háromszögből álló felület egy oktaéder, amelyiknek két szemközti lapját eltávolítottuk, és ez merev a két lap eltávolítása után is (8. ábra).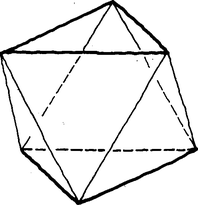
 
 
8. ábra
 

Arra is gondolni kell, hogy a felületnek a feladatbeli leírása (most már 28 helyett 6k darab háromszöggel, ahol k legalább 2) nem egyértelmű, hiszen elkészítve a hálót, a két A1B1 él összeragasztása előtt még meg is csavarhatjuk, akár többször is. A 9. és 10. ábra egy-egy síkba hajtogatott, 6k háromszögből álló szalagot mutat, és alatta ‐ hajlékony anyagból képzelve el őket ‐ térben is szemléltettük alakjukat.
 
 
9. ábra
 

 
 
10. ábra
 

Az már kérdéses, hogy a síkbeli zárt karika 3-dimenziós felületté hajtogatható-e csak a megengedett élek menti hajtogatással. Az, hogy ez nem magától értetődő, látható abból is, hogy az oktaéder-felületnek megfelelő szalag is megvalósítható a síkban. A jobb elképzelés kedvéért két részben rajzoltuk meg a felületet.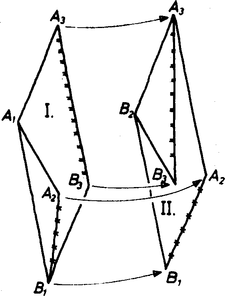
 
 
11. ábra
 

A 11. ábra két rombusza fölé kell hajtani a hozzájuk csatlakozó háromszöget, majd az I rombuszt a II-re helyezni és az egyformán jelölt (és betűzött) éleket összeragasztani. Ha ez 3-dimenziós felületté volna hajtogatható a háromszögek hajlítása nélkül, akkor megfordítva, az oktaéder-felület is síkba volna hajtogatható, de az, mint említettük, merev. Még meglepőbb eredményre jutunk, ha az I rombuszhoz csatlakozó háromszöget a rombusz alá hajtjuk, úgy helyezzük egymásra a két rombuszt és ragasztjuk össze az egymásnak megfelelő éleket. Így egy megcsavart szalagot kapunk síkba hajtogatva (12. ábra). Ennek megfelelő 3-dimenziós felület merev háromszögekből egyáltalán nem készíthető.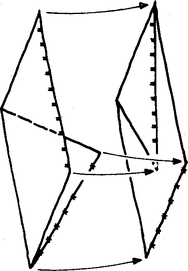
 
 
12. ábra
 

2. Többen állították, hogy a 3k háromszögből álló szalag is síkba hajtogatható, ha k≥2. Ez az állítás már azért is kétes értékű, mert a feladat szövege páros számú háromszögre utal. Megtehetjük azonban, hogy pl. eggyel kevesebb B pontot veszünk, mint A-t. Így már páratlan számú háromszög keletkezik. Ekkor azonban a IV. megoldásra gondolva az ott szereplő élsorozat kijelölt ponttól kijelölt pontig menő három-három éle egy A pontból egy B pontba vezet vagy fordítva. Ha tehát páratlan számú élhármasunk van, akkor az csak úgy zárulhat, ha A1-ből B1-be vezet. A szalagot tehát úgy kell zárnunk, hogy a kezdő A1B1 élet a záró B1A1 éllel ragasztjuk össze. Ilyen módon úgynevezett Möbius-szalagot kapunk, amelyiknek csak egy határvonala és egy oldala van. Ilyen síkba hajtogatott szalag 6k+3 háromszögből mindig készíthető, ha k≥1 (13. áb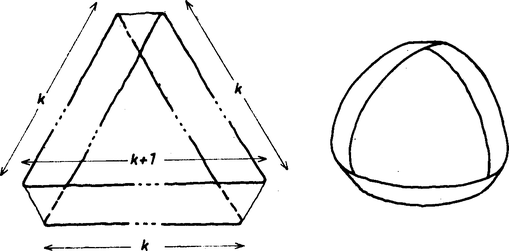ra).
 
 
13. ábra
 

Megjegyzendő, hogy azok a versenyzők, akik akár az 1., akár a 2. megjegyzésben szereplő állítást megfogalmazták, igazolásukra nem tettek kísérletet.