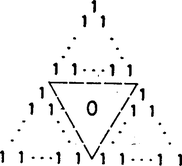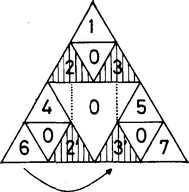Feladat: 1984. évi Kürschák matematikaverseny 1. feladata Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Birkás György ,  Csillag Péter ,  Csizmadia György ,  Erdős László ,  Kós Géza ,  Oláh András ,  Pál Gábor 
Füzet: 1985/február, 51 - 55. oldal  PDF  |  MathML 
Témakör(ök): Binomiális együtthatók, Maradékos osztás, Teljes indukció módszere, Szorzat, hatványozás azonosságai, Számsorozatok, Összefüggések binomiális együtthatókra, Oszthatóság, Kombinatorika, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1985/február: 1984. évi Kürschák matematikaverseny 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. a) Írjunk a Pascal-háromszögben a páratlan számok helyébe 1-et, a párosak helyébe 0-t. Ekkor a hogy két páratlan szám összege páros. A következőkben a módosított háromszöget a módosított képzési szabállyal fogjuk Pascal-háromszögnek nevezni.
Felírva valameddig a háromszöget, a következő szerkezetet vehetjük észre: ha 2n számú sort írunk fel, akkor az utolsó sor csupa 1-esből áll, és a következő 2n sorban két 2n sorból álló Pascal-háromszög keletkezik egymás mellett, közöttük pedig csupa 0 (1. ábra).

 
 
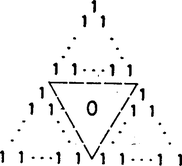1. ábra
 

Belátjuk teljes indukcióval, hogy ez minden n-re igaz.
Világos, hogy n=1-re igaz az állítás (már n=0-ra is).
Tegyük fel, hogy n-nek valamilyen k értékére a 2k-adik sorban csupa 1-es áll, szám szerint 2k darab. Ekkor a következő sor két szélén 1-es áll, köztük pedig 2k-1 darab nulla. A további sorokban a 0-k száma egyesével csökken, a két szélén pedig egy-egy újabb Pascal-háromszög keletkezik egymástól függetlenül addig, míg a köztük levő 0-k el nem fogynak. Ez a 2k-adik lépésben következik be. Az ez alatt kialakult két Pascal-háromszög utolsó sora feltevésünk szerint csupa 1-esből áll, tehát a 2k+1 sorból álló Pascal-háromszög utolsó sora is csupa 1-esből áll. A tulajdonság tehát öröklődik. Ezzel beláttuk, hogy fennáll minden n-re.
 

b) Felírva n néhány kezdő értékére a 2n sorból álló háromszöget, az oszlopok szerinti összegzés a következő eredményeket adja (a fölső sorba a sorok számát, alá az oszlopösszegek páros vagy páratlan voltát jelző 0, 1-ek sorozatát írtuk):
2021222311,1,11,1,0,1,0,1,11,1,0,1,1,0,1,1,1,0,1,1,0,1,1

Azt látjuk, hogy középen mindig 1-es áll, odáig balról 1, 1, 0 ismétlődik periodikusan, jobbról 0, 1, 1; páros hatvány esetén nincs töredék hármas, páratlan hatványnál viszont a középső 1-es mellé még egy-egy hármas első, illetőleg utolsó 1-ese kerül.
Belátjuk teljes indukcióval, hogy az oszlopösszegek szerkezete, ha 2n sorú háromszög oszlopait összegezzük, minden n-re ilyen. Az első néhány n értékre már láttuk, hogy ez igaz.
Az is világos, hogy középen 1-nek kell állnia, akárhány sor után összegezünk is, hiszen a háromszögek a)-ban megállapított szerkezete szerint az első sor egyetlen 1-ese alá a továbbiak során mindig 0 kerül.
Tegyük fel, hogy n valamilyen k értékére igaz az állítás. Összegezzük a 2k+1 sorból álló háromszöget úgy, hogy külön összegezzük az első 2k sort és külön a többit, majd a két keletkező összegsort is összegezzük. Ezt kívántuk jelezni a 2. ábrán. Az a) rész szerint a második sorban kétszer ismétlődik az első sorbeli sorozat; a középső 1-esek az első sor első 1-ese előtti, ill. az utolsó 1-es utáni hely alá kerülnek.
 
 
2. ábra
 

Ha most k páros, akkor az 1, 1, 0 hármasok alá 0, 1, 1 hármasok kerülnek, ill. a jobb oldalon megfordítva. Ezekből összegezve 1, 0, 1 lesz. Így a végeredmény a következő: 1, 1, 0 hármasok következnek az alsó sorban a bal oldali középső 1-esig, majd ez után 1, 0, 1 hármasok. De akkor az elsőhöz hozzácsatolva a középső1-est, továbbra is 1, 1, 0 hármasok következnek, míg a felső sor középső 1-ese előtt marad még külön egy 1-es. Hasonlóan a jobb oldalán is marad egy 1-es, majd 0, 1, 1 hármasok következnek. Ezzel épp a páratlan kitevőre vonatkozó szerkezetet kaptuk.
Ha viszont k páratlan, akkor a fölső sor szélső 1-eseit válasszuk külön. Ezek után 1, 0, 1 hármasok következnek mindkét oldalról egészen a középső 1-esig. A bal oldalon az első 1-es alatt az alsó sorozat középső 1, 1, 1 hármasának az utolsó 1-ese áll, utána pedig az 1, 0, 1 hármasok alatt 0, 1, 1 hármasok. Így összegzéskor csupa 1, 1, 0 hármasokat kapunk a középső 1-esig. Jobbról ennek a tükörképe áll, így ebben az esetben a páros kitevőnek megfelelő szerkezet adódott. Ezzel a bizonyítást befejeztük.
A feladat 210, tehát a páros hatvány számú sor utáni összegezés esetén kérdezi a páratlan oszlopösszegek számát. Ekkor 2046/3 összeghármas keletkezik 2‐2 páratlan összeggel, és ehhez járul még a középső páratlan összeg, ami együtt 1365 páratlan összeget ad.
 

Megjegyzés. Általában ha 2n sor leírása után összegezünk, akkor a keletkező 2n+1-1 összeg közt, ha n páros, eredményünk szerint
2⋅2n+1-23+1=2n+2-13,
páratlan szám van, míg páratlan n esetén a páratlan oszlopösszegek száma
2⋅2n+1-43+3=2n+2+13.
A két eredmény egybefoglalható a következő formulában:
2n+2-(-1)n3.

 
II. megoldás. Az I. megoldás a) részét felhasználjuk. Legyen n≥2 és a 2n+1 számú sor utáni összegzést bontsuk két részre, mint az előző megoldásban, de a fellépő 3 Pascal-háromszög összegzését még bontsuk fel feleakkora háromszögek összegzésére, amint a 3. ábra mutatja.
 
 
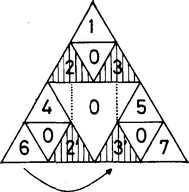3. ábra
 

A 0-kból álló háromszögeket figyelmen kívül hagyhatjuk. Ugyancsak nem kell figyelembe venni a 2 és 2', továbbá a 3 és 3' jelű háromszögeket sem, mert ezekben azonos oszlopok állnak egymás alatt, így összegük mindig páros számot ad. A megmaradó háromszögek közül az 1 jelűnek, a 4 és 6 jelű párnak, továbbá az 5 és 7 jelűből állónak nincs közös oszlopa, így ezekre a részekre külön-külön végezhetjük az összegzést.
Módosítsunk ezen még annyit, hogy a 6 jelű háromszöget áthelyezzük a 3' jelű helyére. Ezzel azok az oszlopai, amelyek a 4 valamelyik oszlopa alatt álltak, az 5 azonos oszlopa alá kerülnek, így az oszlopösszegek nem változnak. Így végül két 2n-1 sorú és egy 2n sorú Pascal-háromszög oszlopait kell összegeznünk. Jelöljük f(n)-nel a, 2n sorú Pascal-háromszög oszlopösszegei közt a páratlan számok számát, akkor meggondolásunk azt adta, hogy
f(n+1)=2f(n-1)+f(n).
Tudva még, hogy f(0)=1, f(1)=3, sorra meghatározhatjuk az egymás utáni helyeken f értékeit. Úgynevezett rekurzív meghatározást nyertünk f értékeire. f(10)-re természetesen ismét 1365 adódik.
Megjegyezzük, hogy a közbenső függvényértékeket megfigyelve ebből is megsejthetjük, és a nyert összefüggés alapján teljes indukcióval bebizonyíthatjuk a fenti megjegyzésben nyert formulát f(n)-re.
 

III. megoldás. Meggondolásunkat kicsit egyszerűsíti az a megjegyzés, hogy a Pascal-háromszög sorait folytathatjuk mindkét irányban nullákkal. Ekkor az egy 1-est és kívüle csupa 0-t tartalmazó első sorból elindulva a továbbiak mind úgy keletkeznek, hogy az egyes helyekre a balra és jobbra fölöttük levő szám összegét írjuk.
Megvizsgáljuk, hogy ha valamelyik soránál megállva oszloponként összegezzük az egymás alatt álló számokat, milyen kapcsolat olvasható le ebből a képzési szabályból az egymás mellett álló összegekre. Nézzük először a középső oszlopot. Erre tükrös a Pascal-háromszög, hiszen ha tükrözünk rá, az első sor sem változik meg és a képzési szabály is érvényben marad. Ebben az oszlopban legfelül az első sor egyetlen 1-ese áll, alatta csupa páros szám, hiszen mindegyik két tükrös helyzetű, tehát egyenlő szám összege. A középső oszlop összege tehát akármelyik sorig páratlan szám.
Ha a középsőtől különböző olyan oszlopot nézünk, amelyiknek van eleme az utolsó sorban, akkor az oszlop minden eleme a két szomszédos oszlop egy-egy elemének az összege, és a szomszédos oszlopok minden eleme szerepel összeadandóként. Így a kérdéses oszlopösszeg a két szomszédos oszlopösszegnek az összegével egyenlő. Az olyan oszlopokra, amelyeknek az utolsó eleme az utolsó előtti sorban áll, megállapításunk akkor volna érvényes ha még egy sor kiírása után végeznénk az összegezést. Az ilyen oszlopösszegek tehát a szomszédos oszlopösszegek összegénél kisebbek a következő sornak a kérdéses oszlopba eső elemével.
A Pascal-háromszög m-edik sorában a 0-tól különböző számok az (m-1k), 0≤k≤m-1 binomiális együtthatók. Ezekre fennáll a következő összefüggés (lásd az alábbi 1. megjegyzést):
m⋅(m-1k-1)=(mk)⋅k(1)

Ha 2-hatvány sorszámú sor után végezzük az összegezést, akkor az összegekre talált összefüggés szerint a következő sor elemeinek a párosságát kell ismernünk. Belátjuk azonban, hogy ennek minden eleme páros a két szélen álló 1-es kivételével, s így levonása nem változtatja meg az összeg páros vagy páratlan voltát. Valóban, az (1) összefüggésből, ha m=2n, akkor a jobb oldalnak is oszthatónak kell lennie 2n-nel. Mivel pedig k a 2-nek csak n-nél alacsonyabb hatványával lehet osztható, mert 1≤k≤2n-1, így (2nk) is páros kell hogy legyen.
A középső oszlopra vonatkozó szimmetria miatt elég azt megállapítani, hogy az az előtti oszlopok összegei között hogyan oszlanak el a páros és páratlan összegek.
Az első nem csupa 0-ból álló oszlop utolsó eleme 1, afölött csupa 0 áll, így az összeg is 1, tehát páratlan. Mivel az előtte álló oszlopösszeg 0, az utána állónak páratlannak kell lennie, hogy az összegük 1 legyen. A következő oszlopösszeg páros, mert közte és az első oszlop között páratlan összegű oszlop áll. A levonandó következő sorbeli elem, mint láttuk, az összeg párosságát nem változtatja meg. Ez után viszont újra páratlan összeg következik, mert a kettővel előbbi páratlan összeghez adva, páros eredményt kell adnia. Ezzel a kiindulási helyzethez: páros összeg után páratlan, jutottunk vissza, s így ismétlődik, amit eddig találtunk: páratlan, páratlan, páros összegek következnek egészen a középső előtti oszlopig, a középsőben mindig páratlan az összeg, onnan pedig az odáig talált összegek következnek fordított sorrendben.
Ezzel az I. megoldás b) részében talált eredményre jutottunk, amiből az ott látott módon következtethetünk tovább.
 

Megjegyzések 1. Az (1)összefüggés könnyen nyerhető számítással, de belátható kombinatorikus meggondolással is. Egy m-tagú társaság k-tagú küldöttséget akar kijelölni, köztük egy szószólóval. Ekkor kiválaszthatják a szószólót m-féleképpen és mellé a k-1 tagot a maradó m-1-ből (m-1k-1)-féleképpen. Így a bal oldali kifejezés adódik a lehetőségek számára. Eljárhatnak azonban úgy is, hogy kiválasztják a k embert (mk)-féleképpen, és azok maguk közül választanak egy szószólót, ami k-féleképpen lehetséges. Így a jobb oldal is ugyanezeknek a lehetőségeknek a számát adja.
2. A fentiekhez hasonlóan 2 helyett tetszés szerinti p prímszámra és pozitív egész n-re lehet látni (1)-ből, hogy (pnk) osztható p-vel, ha 1≤k≤pn-1. Ebből viszont a képzési szabály alapján következik, hogy az előző sor számai felváltva 1 és p-1 maradékot adnak p-vel osztva. Ennél valamivel több is igaz: ha 1≤a≤p-1, akkor (apn-1k) nem osztható p-vel. Ezt úgy látjuk be, mivel tudjuk, hogy egész számról van szó, hogy felírjuk olyan tört alakjában, amelyiknek a számlálója egyszerűsítés után nem osztható p-vel:
(apn-1k)=apn-11⋅apn-22⋅...⋅apn-kk.

Itt a választása miatt a kivonandó p-nek legfeljebb akkora hatványával osztható, mint a kisebbítendő (ez lehet természetesen a 0-adik hatvány is), tehát a különbség akkora hatványával, mint a kivonandó, ami egyben a nevező is. Ekkor azonban egyszerűsítés után a szorzat számlálója valóban nem osztható p-vel (természetesen a nevező sem).