Kezdőlap


Feladat:	1982. évi Kürschák matematikaverseny 1. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Hetyei Gábor , Magyar Ákos
Füzet:	1983/február, 50 - 53. oldal		PDF \| MathML
Témakör(ök):	Rácsgeometria, Térgeometria, Kocka, Vektorok, Vektorok skaláris szorzata, Vektorok lineáris kombinációi, Racionális számok és tulajdonságaik, Természetes számok, Prímtényezős felbontás, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):	Feladatok: 1983/február: 1982. évi Kürschák matematikaverseny 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Fel fogjuk használni ‐ amit a megjegyzések keretében be is bizonyítunk ‐, hogy az r( $r_{1}$ , $r_{2}$ , $r_{3}$ ) és az u( $u_{1}$ , $u_{2}$ , $u_{3}$ ) koordinátáival adott két vektor akkor és csak akkor merőleges, ha

\begin{matrix} r_{1} u_{1} + r_{2} u_{2} + r_{3} u_{3} = 0. \end{matrix}

Legyenek egy

A B C D E F G H

kocka egy lapjának

A

B

C

D

csúcsai egész koordinátájúak, a kocka élének hossza a szintén egész szám, az

A

-val szomszédos harmadik csúcs

E

. Azt kell belátnunk, hogy

E

F

G

H

is egész koordinátájú. Elég belátnunk, hogy pl. az

\vec{A E}

vektor koordinátái egész számok, hiszen

E

F

G

H

koordinátáit úgy kaphatjuk, hogy

A

B

C

, ill.

D

koordinátáihoz hozzáadjuk

\vec{A E}

koordinátáit.

Legyenek az

\vec{A B} = b

\vec{A D} = d

\vec{A E} = e

koordinátái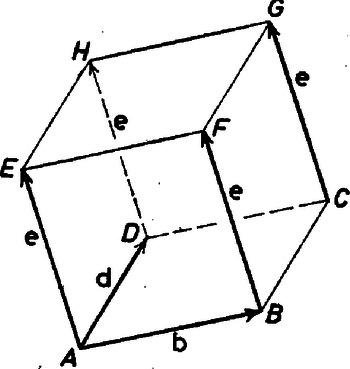

\begin{matrix} (b_{1}, b_{2}, b_{3}), (d_{1}, d_{2}, d_{3}), ill (e_{1}, e_{2}, e_{3}) . \end{matrix}

Ezeket úgy kaphatjuk, hogy a

B

D

, ill.

E

pont koordinátáiból kivonjuk

A

koordinátáit. A b és d vektor koordinátái tehát egész számok, és azt kell belátnunk, hogy e koordinátái is azok. A b és d vektorok hossza

a

, és a vektorok merőlegesek, tehát koordinátáikra teljesül, hogy

\begin{matrix} (1) b_{1}^{2} + b_{2}^{2} + b_{3}^{2} = a^{2}, (2) d_{1}^{2} + d_{2}^{2} + d_{2}^{3} = a^{2}, (3) b_{1} d_{1} + b_{2} d_{2} + b_{3} d_{3} = 0. \end{matrix}

Az e vektor merőleges b-re is, d-re is és

a

hosszúságú, tehát

\begin{matrix} b_{1} e_{1} + b_{2} e_{2} + b_{3} e_{3} = 0, \\ e_{1}^{2} + e_{2}^{2} + e_{3}^{2} = a^{2} . \\ d_{1} e_{1} + d_{2} e_{2} + d_{3} e_{3} = 0, \end{matrix}

Az első két egyenletből kifejezhetjük

e_{1}

e_{2}

e_{3}

-at, de ezt a 3 adatot a két egyenlet csak egy

k

közös szorzó tényező erejéig határozza meg.A számításokat elvégezve azt kapjuk, hogy

\begin{matrix} e_{1} = k (b_{2} d_{3} - b_{3} d_{2}), e_{2} = k (b_{3} d_{1} - b_{1} d_{3}), e_{3} k (b_{1} d_{2} - b_{2} d_{1}) . \end{matrix}

A vektor hosszát kiszámítva

\begin{matrix} a^{2} = k^{2} {b_{2}^{2} d_{3}^{2} + b_{3}^{2} d_{2}^{2} + b_{3}^{2} d_{1}^{2} + b_{1}^{2} d_{3}^{2} + b_{1}^{2} d_{2}^{2} + b_{2}^{2} d_{1}^{2} - 2 b_{2} d_{2} b_{3} d_{3} - 2 b_{1} d_{1} b_{3} d_{3} - 2 b_{1} d_{1} b_{2} d_{2}} . \end{matrix}

(4)

Bontsuk a kivonandókat 2‐2 egyenlő tag összegére és a másik két tag egyikének, ill. másikának egyik részével közös tényezőket emeljük ki. Ekkor a kivonandó így alakul

\begin{matrix} - b_{2} d_{2} b_{3} d_{3} - b_{3} d_{3} b_{1} d_{1} - b_{2} d_{2} b_{3} d_{3} - b_{2} d_{2} b_{1} d_{1} - b_{1} d_{1} b_{2} d_{2} - b_{1} d_{1} b_{3} d_{3} = \\ = - b_{3} d_{3} (b_{1} d_{1} + b_{2} d_{2}) - b_{2} d_{2} (b_{3} d_{3} + b_{1} d_{1}) - b_{1} d_{1} (b_{2} d_{2} + b_{3} d_{3}) = \\ = - b_{3} d_{3} (- b_{3} d_{3}) - b_{2} d_{2} (- b_{2} d_{2}) - b_{1} d_{1} (- b_{1} d_{1}) . \end{matrix}

Az utolsó lépésben mindhárom tag második tényezőjére a (3) összefüggést alkalmaztuk. Eredményünket (4)-be beírva azt kapjuk, hogy

\begin{matrix} a^{2} = k^{2} {b_{2}^{2} d_{3}^{2} + b_{3}^{2} d_{2}^{2} + b_{3}^{2} d_{1}^{2} + b_{1}^{2} d_{3}^{2} + b_{1}^{2} d_{2}^{2} + b_{2}^{2} d_{1}^{2} + b_{3}^{2} d_{3}^{2} + b_{2}^{2} d_{2}^{2} + b_{1}^{2} d_{1}^{2}} = \\ = k^{2} {(b_{1}^{2} + b_{2}^{2} + b_{3}^{2}) (d_{1}^{2} + d_{2}^{2} + d_{3}^{2})} = k^{2} a^{4}, k^{2} = \frac{1}{a^{2}} . \end{matrix}

Az e vektor koordinátái tehát:

\begin{matrix} \frac{b_{2} d_{3} - b_{3} d_{2}}{a}, \frac{b_{3} d_{1} - b_{1} d_{3}}{a}, \frac{b_{1} d_{2} - b_{2} d_{1}}{a}, \end{matrix}

vagy ezek ellentettjei. Világos, hogy ezek racionális számok, azt kell belátnunk, hogy egészek.
Elég ezt a fenti hármasról belátni, mert egész szám ellentettje is egész. Elég továbbá egyik koordinátáról belátni, hogy az egész, mert akkor az indexek alkalmas cseréjével adódik a másik kettő egész voltának a bizonyítása.
Azt fogjuk belátni, hogy a koordináta négyzete egész szám. Tudjuk, hogy ha egy racionális szám négyzete egész szám, akkor az alap is egész szám. Az első koordináta számlálójának négyzetét fogjuk átalakítani:

\begin{matrix} {(b_{2} d_{3} - b_{3} d_{2})}^{2} = b_{2}^{2} d_{3}^{2} + b_{3}^{2} d_{2}^{2} - 2 b_{2} d_{2} b_{3} d_{3} = \\ = b_{2}^{2} d_{3}^{2} + b_{3}^{2} d_{2}^{2} - b_{2} d_{2} (- b_{1} d_{1} - b_{2} d_{2}) - b_{3} d_{3} (- b_{3} d_{3} - b_{1} d_{1}) = \\ = b_{2}^{2} d_{3}^{2} + b_{3}^{2} d_{2}^{2} + b_{1} d_{1} b_{2} d_{2} + b_{2}^{2} d_{2}^{2} + b_{3}^{2} d_{3}^{2} + b_{1} d_{1} b_{3} d_{3} = \\ = b_{2}^{2} d_{3}^{2} + b_{3}^{2} d_{2}^{2} + b_{2}^{2} d_{2}^{2} + b_{3}^{2} d_{3}^{2} + b_{1} d_{1} (b_{2} d_{2} + b_{3} d_{3}) = \\ = (b_{2}^{2} + b_{3}^{2}) (d_{2}^{2} + d_{3}^{2}) - b_{1}^{2} d_{1}^{2} = (a^{2} - b_{1}^{2}) (a^{2} - d_{1}^{2}) - b_{1}^{2} d_{1}^{2} = a^{2} (a^{2} - b_{1}^{2} - d_{1}^{2}) . \end{matrix}

Itt ismét két tagra bontottuk a kivonandót és egyszer az első, másszor a második két tényező szorzatát helyettesítettük a (3) összefüggésből adódó értékével, majd alkalmaztuk (1)-et, (2)-t és mégegyszer (3)-at.
Azt nyertük tehát, hogy

\begin{matrix} {(\frac{b_{2} d_{3} - b_{3} d_{2}}{a})}^{2} \end{matrix}

egész szám, és ebből ‐ mint már említettük ‐ következik az alap egész volta is. Ezzel a feladat állítását bizonyítottuk.

Megjegyzések. 1. A megoldás elején kimondott állítás így látható be: Az, hogy

r

és

u

merőleges egymásra, azt jelenti, hogy az

O R U

háromszög derékszögű (a 2. ábra betűzését használjuk), ez pedig egyenértékű állítás azzal, hogy a háromszög oldalaira teljesül Pitagorász tétele. Az r‐ u vektor koordinátái (

r_{1} - u_{1}

r_{2} - u_{2}

r_{3} - u_{3}

), így a feltételt koordinátákkal felírva

\begin{matrix} r_{1}^{2} + r_{2}^{2} + r_{3}^{2} + u_{1}^{2} + u_{2}^{2} + u_{3}^{2} = {(r_{1} - u_{1})}^{2} + {(r_{2} - u_{2})}^{2} + {(r_{3} - u_{3})}^{2} = \\ = r_{1}^{2} + r_{2}^{2} + r_{3}^{2} + u_{1}^{2} + u_{2}^{2} + u_{3}^{2} - 2 (r_{1} u_{1} + r_{2} u_{2} + r_{3} u_{3}) . \end{matrix}

Ez pedig valóban egyenértékű azzal, hogy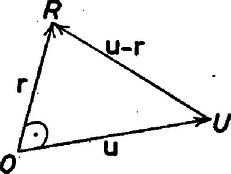

\begin{matrix} r_{1} u_{1} + r_{2} u_{2} + r_{3} u_{3} = 0. \end{matrix}

2. Aki ismeri a vektorok skaláris szorzatát, annak a most levezetett összefüggés jól ismert, aki pedig a vektoriális szorzatot is ismeri, az tudja, hogy az e vektor koordinátáiban

k

szorzói a vektorszorzat koordinátái, és azt is, hogy merőleges vektorok vektorszorzatának a hossza a tényezők hosszának a szorzata, esetünkben tehát

a^{2}

. Így

k

vagy

\frac{1}{a}

vagy

- \frac{1}{a}

. Ezeket felhasználva lényegesen lerövidül a megoldás.

3. A bizonyítás végén felhasznált tétel: ha egy racionális szám négyzete egész, akkor az alap is egész, a számelmélet alaptételének a következménye. E tétel szerint az egész számok törzstényezőkre bontott alakjában a tényezők sorrendtől eltekintve egyértelműen vannak meghatározva.
Valóban, ha egy

v / w

tört (

v, w

egész) nem egész szám, akkor

w

-nek van olyan

p

törzstényezője, ami

v

felbontásában kisebb hatványon szerepel, mint

w

-ében (esetleg egyáltalán nem szerepel). De

\begin{matrix} {(\frac{v}{w})}^{2} = \frac{v^{2}}{w^{2}} . \end{matrix}

Az alaptétel szerint

v^{2}

-nek és

w^{2}

-nek nincs más prímtényezős felbontása, mint amelyik a

v

, ill.

w

felbontásában szereplő prímek hatványkitevőinek kétszerezésével keletkezik. Ekkor azonban

p

v^{2} / w^{2}

tört nevezőjében is magasabb hatványon szerepel, mint, a számlálóban, tehát ez a tört sem lehet egész szám.