Feladat: 1981. évi Kürschák matematikaverseny 1. feladata Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Bali János ,  Dósa György ,  Gellér János ,  Király Zoltán ,  Magyar Ákos ,  Nacsa János ,  Simonyi Gábor ,  Szabó Endre ,  Szenes András ,  Tardos Gábor 
Füzet: 1982/február, 50 - 53. oldal  PDF  |  MathML 
Témakör(ök): Geometriai egyenlőtlenségek, Háromszögek nevezetes tételei, Négyszögek geometriája, Háromszög-egyenlőtlenség alkalmazásai, Gömbi geometria, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1982/február: 1981. évi Kürschák matematikaverseny 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Mielőtt a tulajdonképpeni megoldásra térnénk, megjegyezzük, hogy a feladat szövege nem zárja ki, hogy a pontok közül több, akár mind az 5 egy egyenesre essék, sőt a bizonyítandó egyenlőtlenség még akkor is érvényes, ha több pont egybeesik. Ha egy K és L pont egybeesik, akkor a KL (zárt) szakaszon a K(=L) pontot értjük, a hossza pedig 0. A háromszög-egyenlőtlenség továbbra is érvényes a következő alakban: a tetszés szerinti K, L, M ponto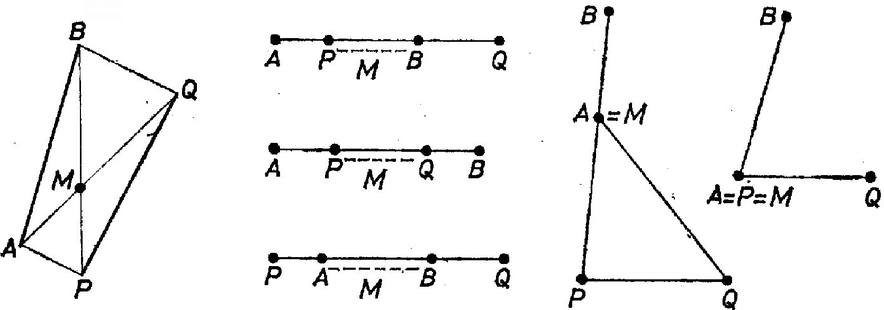kra

KL¯+KM¯≥LM¯,
és itt abban az esetben érvényes az egyenlőség jele, ha K az LM szakasz pontja.
 

1. ábra
 

A feladatra térve, annak állítását az említett legáltalánosabb értelmezés mellett bizonyítjuk. Két esetet különböztetünk meg. Az első, ha a P, Q, R pontok között van kettő, mondjuk P és Q, amelyekre az AQ és BP szakaszoknak van egy M közös pontja (1. ábra.) Ez más szóval azt jelenti, hogy ABQP konvex négyszög, amely egyenes szakasszá is fajulhat, ha a négy pont egy egyenesen van, vagy háromszöggé, ha három pont egy egyenesen van; esetleg két szomszédos csúcs egybeesik. Ilyenkor MAB-re és MPQ-ra alkalmazva a háromszög-egyenlőtlenséget
MA¯+MB¯≥AB¯,MP¯+MQ¯≥PQ¯.
Itt
MA¯+MQ¯=AQ¯,MB¯+MP¯=BP¯,
így a két egyenlőtlenség megfelelő oldalait összeadva azt nyerjük, hogy
AQ¯+BP¯≧AB¯+PQ¯.

Bárhol fekszik is az R pont, APR-re és BQR-re alkalmazva a háromszögegyenlőtlenséget
AP¯+AR¯≥PR¯,BQ¯+BR¯≥QR¯.
Az utolsó három egyenlőtlenség megfelelő oldalait összeadva a bizonyítandó összefüggést kapjuk.
Az olyan eseteket kell még megvizsgálnunk, amelyekben bármely kettőt jelenti is U és V a P, Q, R pontok közül, AU-nak és BV-nek nincs közös pontja. Ez esetben mind az 5 pont különböző, és sem PQ, sem QR, sem PR nem párhuzamos AB-vel. Ha ugyanis A és B, vagy A és P, vagy B és Q, vagy P és Q egybeesnék, vagy ha PQ és AB egy irányban párhuzamos volna, akkor AQ-nak és BP-nek volna közös pontja, az első négy esetben éppen az egybeeső pontpár.
A P, Q, R pontok közül legalább kettő az AB egyenesnek ugyanarra a partjára vagy az egyenesre esik. Jelöljük ezek közül a távolabbit, illetőleg a legtávolabbit P-vel, a másikat Q-val, ha pedig R is erre az oldalra esik, az legyen az AB egyeneshez legközelebbi. Ekkor a PQ egyenes belső pontban metszi az AB szakaszt, mert különben ABPQ vagy ABQP konvex négyszög volna, s így átlóinak volna közös pontja.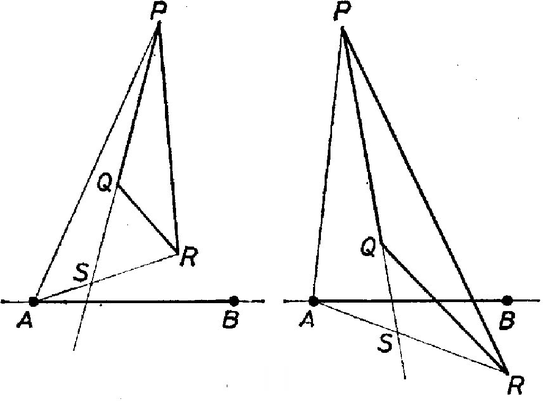

2. ábra

Ha P, Q, R nincs egy egyenesen, feltehetjük, hogy a PQ egyenes elválasztja A-t és R-et (2. ábra). Ekkor az APR háromszög tartalmazza (belsejében vagy a határán) Q-t. AR és PQ metszéspontját jelöljük S-sel. Alkalmazzuk a háromszög-egyenlőtlenséget az APS háromszögre (ez nem elfajuló, mert A nincs a PS egyenesen), és SQR-re:
AP¯+AS¯>PS¯,SQ¯+SR¯≥QR¯.
Itt
AS¯+SR¯=AR¯,PS¯=PQ¯+SQ¯.
A két egyenlőtlenség megfelelő oldalait összeadva, figyelembe véve a két egyenlőséget és mindkét oldalról elhagyva a QS¯ távolságot, azt kapjuk, hogy
AP¯+AR¯>PQ¯+QR¯.
(Mivel az egyik esetben nem állhat fenn egyenlőség, így az összeadással keletkezett egyenlőtlenségben sem.)
Alkalmazzuk a háromszög-egyenlőtlenséget QAB-re és BPR-re:
QA¯+QB¯≥AB¯,BP¯+BR¯≥PR¯.
Az utolsó három egyenlőtlenség megfelelő oldalait összeadva ebben az esetben is a bizonyítandó egyenlőtlenséget kapjuk. Ezzel a feladat állítását bebizonyítottuk.
 

Megjegyzések. 1. A bizonyítás során a háromszög-egyenlőtlenség következő két következményét bizonyítottuk be és használtuk fel:
a) Konvex négyszög átlói hosszának az összege nagyobb, mint két szemközti oldal hosszának az összege.
b) Ha az ABC háromszög tartalmazza a D pontot, de D különbözik A-tól, akkor
AB¯+AC¯>DB¯+DC¯.
Mindkét állítás igaz elfajuló sokszögekre is, ha ,,nagyobb'' helyett ,,nagyobb vagy egyenlőt'' mondunk. Az első állításban, ha két szomszédos csúcs egybeesik, akkor az ebből a pontból a másik két pontba vezető szakaszok szemben fekvő oldalaknak számítanak, de egyben ezek a négyszög átlói is. Így ha ezt a két szemben fekvő oldalt vesszük, akkor egyenlőség áll fenn. (Ha a másik két szemben fekvő oldalt tekintjük, azok közül az egyik 0 hosszúságú, s így a háromszög-egyenlőtlenséget kapjuk.) A bizonyítást elemezve láthatjuk, hogy még egy esetben áll fenn egyenlőség: ha a négy pont egy egyenesen van, a szemközti oldalpárnak tekintett két szakasz egyirányú és van közös pontjuk.
Mindkét alakzat a második állítás elfajuló esetének is tekinthető: az előbbi annak a fönt kizárt esetnek, ha D egybeesik A-val, a második pedig annak, amikor a háromszög csúcsai egy egyenesen vannak, továbbá A és D a BC szakasz pontjai. A bizonyítást elemezve látható, hogy csak ezekben az esetekben állhat fenn egyenlőség.
2. Nézzük meg, a feladat állításában mikor állhat fenn egyenlőség. Láttuk, hogy a bizonyítás második részében ez nem következhet be, mert az első rész-egyenlőtlenségben nem állhat fenn egyenlőség.
A bizonyítás első részében a négyszögre vonatkozó egyenlőtlenségben akkor áll fenn egyenlőség, ha A és P egybeesik (ettől nem lényegesen különböző eset, ha B és Q esik egybe) vagy ha AB és PQ egy egyenesnek két egyirányú szakasza, amelyeknek van közös pontjuk (a 0 hosszúságú szakaszt minden szakasszal párhuzamosnak és egyirányúnak tekintjük). A további két egyenlőtlenségben akkor lesz az egyenlőség jele érvényes, ha A a PR szakasznak, B pedig a QR szakasznak pontja.
Ha A és P egybeesik, akkor az utolsó előtti követelmény R helyzetétől függetlenül teljesül, így akkor lesz a feladat állításában az egyenlőség jele érvényes, ha R a QB szakasz B-n túli meghosszabbításán van. Egyik lehetőségnek azt kaptuk tehát, hogy A és B egyike a PQR háromszög egyik csúcsával esik egybe, a másik pedig a szemközti oldalszakasz pontja.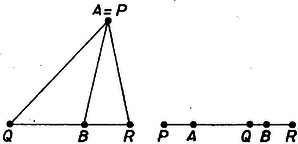

3. ábra

Ha A,B,P és Q egy egyenesen van, akkor az utolsó két követelmény akkor és csak akkor teljesül, ha R is ezen az egyenesen van, továbbá A és B a másik három pont közti két, közös belső pont nélküli szakasz egyikének, ill. másikának pontja (3. ábra).
3. Általánosan igaz, hogy ha A1,A2,...,An és B1,B2,...,Bn+1 egy sík pontjai, akkor az A-k közti szakaszok és a B-k közti szakaszok hosszának összege nem nagyobb, mint az összes AiBj távolságok összege. n=1-re a háromszög-egyenlőtlenséget kapjuk; az n=2 eset bizonyítása volt a kitűzött feladat. Nagyobb n értékek esetére egy hasonló jellegű bizonyítási kísérlet áttekinthetetlenné válnék. A gömb már több lehetőséget kínál a rá vonatkozó megfelelő állítás bizonyítására. Ez után a sugár minden határon túli növelésével látható be, hogy az állításnak a síkban is igaznak kell lennie. Ennek a részleteibe azonban nem bocsátkozunk bele.