Feladat: 1980. évi Kürschák matematikaverseny 3. feladata Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Bohus Géza ,  Horváth István ,  Szabó László ,  Tardos Gábor ,  Tőri Zoltán 
Füzet: 1981/február, 57 - 61. oldal  PDF  |  MathML 
Témakör(ök): Kombinatorika, Játékelmélet, játékok, Kombinatorikai leszámolási problémák, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1981/február: 1980. évi Kürschák matematikaverseny 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

3. feladat. Adott teniszversenyzők két csoportja: az egyik 1000, a másik 1001 versenyzőből áll. Mindegyik csoporton belül ismerjük a versenyzők erősorrendjét. Adjunk meg olyan eljárást, amelynek segítségével 11 mérkőzés lejátszása után megállapítható, ki a 2001 játékos közül a középső (tehát az 1001-edik). (Feltesszük, hogy a játékosok mind különböző erősségűek, és az erősebb játékos mindig legyőzi a gyengébbet.)

 

A teniszezők csoportjait nagybetűkkel fogjuk jelölni, az egyes versenyzőket a megfelelő kisbetűvel, indexként melléírva, hogy a legerősebbtől kezdve hányadik erősségben a saját csoportján belül.
 

I. megoldás. A játszmákat úgy kell választanunk, hogy eredményük alapján minél erősebben szűkíthessük azoknak a körét, akik közt az összesített sorrendben 1001-edik teniszező lehet. Ha egy A és egy B csoport összesített sorrendjében a k-adik versenyzőt keressük, akkor egy később alkalmasan választandó i értékkel ai-t és bk-i-t küldjük pályára. Ekkor a győztesnél csak azok lehetnek jobbak, akik ai-nél is, bk-i-nél is jobbak (8. ábra), a vesztesnél pedig még a győztes is, tehát eggyel több teniszező.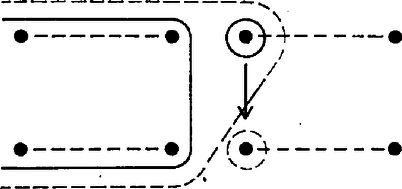
 

8. ábra
 

A győztesnél tehát legfeljebb (i-1)+(k-i-1)=k-2 erősebb versenyző lehet. Így ő a (k-1)-edik vagy annál erősebb az összesített sorrendben. A k-adik helyre tehát nem jön szóba, a nála erősebbek természetesen szintén nem. A vesztesnél legalább eggyel több versenyző erősebb, tehát legalább k-1. Így ő még esetleg lehet k-adik, de a nála gyengébbek már nem. A 9. ábrán a nyíl a győztestől mutat a vesztesre. A zárójelbe tett versenyzők nem lehetnek már k-adika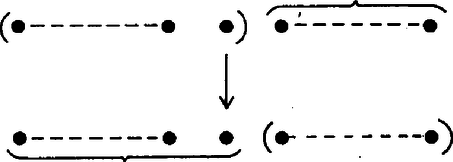k.
 

9. ábra
 

Ha az A csapatban 2n+1 versenyző van, a B-ben 2n, tehát az összsorrendben 2n+1-edik versenyzőt keressük. Válasszuk i-t n+1-nek, tehát küzdjön meg an+1 és bn. Ha an+1 az erősebb, akkor a 2n+1-edik versenyző an+2, ..., a2n+1 és b1, ..., bn közül kerül ki, és ezeket állítva sorrendbe, köztük őt az n-edik helyen találjuk, hiszen a1, ..., an+1-et azért hagyhatjuk figyelmen kívül, mert biztosan erősebbek a 2n+1-edik versenyzőnél.
Ha viszont bn erősebb an+1-nél, akkor a középső versenyző a1, ..., an+1 és bn+1, ..., b2n közül kerül ki, tehát egy n+1 és egy n fős csoport teniszezői közül, és köztük ő az n+1-edik, azaz középső, hiszen n olyan teniszezőt hagytunk figyelmen kívül, akik biztosan erősebbek nála.
Az első esetben 2 versenyző tekinthető középsőnek, közülük az erősebbet kell keresnünk.
Ha A-ban 2n versenyző van, B-ben 2n-1, és az összesített sorrendben a 2n-ediket keressük, akkor an és bn mérje össze erejét. Aszerint, hogy an vagy bn győz-e, an+1, ..., a2n és b1, ..., bn közül, vagy pedig a1, ..., an és bn+1, ..., b2n-1 közül kell keresnünk az n-ediket, tehát két n tagú csoportból az erősebb középsőt, vagy egy n és egy n-1 tagú csoportból a középsőt.
Meg kell vizsgálnunk két egyenlő létszámú csoport esetét is, mert láttuk, ilyenre is vezethet eljárásunk. Ilyen esetekben idáig a két középen levő versenyző közül az erősebbet kellett keresni.
Ha A is, B is 2n tagú és a 2n-edik versenyzőt keressük, akkor an és bn csapjon össze. Az A és B csoport szerepe most teljesen szimmetrikus, elég tehát azt az esetet vizsgálni, ha an győz. Ekkor an+1, ..., a2n és b1, ..., bn közül kell az n-ediket keresnünk, tehát két egyenlő csoport egyesített listáján az erősebbik középsőt.
Ha végül A is, B is 2n+1 versenyzőből áll, és az összesítésben 2n+1-edik versenyzőt keressük, akkor kézenfekvő, hogy eddigi formulánktól kissé eltérve a két középsőt: an+1-et és bn+1-et küldjük pályára. Ismét elég azt az esetet vizsgálni, ha an+1 győz (10. ábra).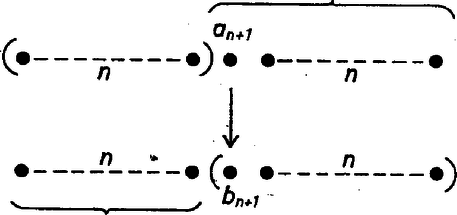
 

10. ábra
 

Ekkor n csoporttársa gyengébb nála, B-ből pedig legalább n+1-en, tehát az erőlistán 2n+1-edik még lehet, de az őt megelőző csoporttársai már megelőzik a 2n+1-edik versenyzőt. bn+1-nél n csoporttársa erősebb és A-ból legalább n+1 teniszező, tehát ő legalább 2n+2-edik, a nála gyengébb csoporttársai pedig még hátrább vannak. Így an+1, ..., a2n+1 és b1, ..., bn közül kell még kiválasztani az n+1-ediket, vagyis egy n+1-es és egy n-es csoportból ismét a középsőt.
Minden esetben azt kaptuk tehát, hogy a versenyzők összlétszáma egy‐egy lépésben megfeleződik, vagy ha páratlan volt, a rosszabbik esetben féllel több lesz a felénél. Eszerint 2001 versenyző esetén eljárásunk mellett az egyes játszmák eredménye a legrosszabb esetben a következőképpen alakulhat: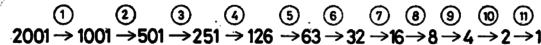

 
 

Legkésőbb a 11-edik lépés után tehát kiderül, ki a középső. Ezzel igazoltuk a feladat állítását.
 

Megjegyzések. 1. Minden lépés után felírva a két csoport lehetséges alakulását, a következő táblázatot kapjuk:

Eszerint eljárásunk a legszerencsésebb esetben is csak 10 lépésben vezet célhoz.
2. A 11-es szám optimális abban az értelemben, hogy nem lehetséges olyan algoritmus, amelyik 10 lépésben megtalálja a középső versenyzőt, bárki legyen is az. Ez azért van így, mert van 2001 versenyző, akik közül bárki lehet a középső. Másrészt viszont csak egy a és egy b-beli játékost van értelme játszatni egymással, mert egy csoportbelieknél tudjuk már a játszmák kimenetelét. Egy‐egy játszmában vagy az A-beli vagy a B-beli játékos győz, tehát kétféle kimenetel lehetséges. A 10 játszmának együtt eszerint 210=1024 különböző kimenetele lehet. Semmilyen algoritmus esetén sem kaphatunk 10 mérkőzésből 2001 különböző választ.
3. Váratlannak látszik, hogy a két páratlan csoport esetében változtatni kellett a stratégián. Akkor lesz ai, a k-adik, ha bk-i-től (ha k>i) kikap, de bk-i+1-et (ha B-ben van legalább k-i+1 játékos) már megveri. A fenti eljárásban a két itt említett játszmából mindig az előbbi típusút játszattuk le, a mondott esetben azonban az utóbbi típusú volt a célszerű. Érdekes megjegyezni, hogy a két típusú játszma minden esetben egymásba megy át, ha ahelyett, hogy a legerősebbtől kiindulva rangsorolnánk a versenyzőket, a leggyengébbtől sorszámoznánk, és "gyengébb''-et és "erősebb''-et mindenütt felcserélnénk, kivéve egyedül azt az esetet, amikor két egyenlő páratlan létszámú csoportnál keressük a középsők közül akár az erősebbet, akár a gyengébbet.
4. Sok versenyző a szimmetria kedvéért úgy hagyott el mindig versenyzőket, hogy páratlan számú versenyző maradjon vissza, és azok közül ismét a középsőt kelljen keresni. A leírt eljárástól tehát annyiban tért el, hogy amikor két különböző létszámú csoportból elég volt csak két egyenlő létszámú részt megtartani, akkor még az éppen lejátszott mérkőzés győztesét is visszatartotta. Ilyen módon 2n+1 és 2n versenyzőből mindig n+1 és n marad vissza, 2n és 2n-1-ből viszont a kedvezőtlenebb esetben két n-es csoport helyett szintén n+1 és n, összlétszámban tehát 4n-1-ből is, 4n+1-ből is 2n+1. Az egyes mérkőzések után eszerint így alakulna az összlétszám:
 
 


Itt egy 1-es és egy 2-es csoport maradt. Ha az egyedül levő győz az erősebb partner ellen, akkor a vesztes a középső, de ha nyer, akkor még a gyöngébbel is meg kell mérkőznie. (A győztes bennhagyása összesen 3 játékos esetén nem vezetne csökkenéshez, így el kell térni az általános előírástól.) Az ötödik lépésben nem lépünk át 2 egy hatványán, és emiatt lehet szükség egy 12-ik játszmára is.
Itt 1 tényleges versenyző fölösleges bennhagyása már elrontotta az algoritmust, viszont ha ügyesebben csináljuk, sok "kitalált'' játékost is hozzávehetünk a meglevőkhöz, és ezzel nem rontjuk, csak egyszerűsítjük a helyzetet. Erre a gondolatra többen is rájöttek, de igazán jól csak Tardos Gábor használta ki.
 

II. megoldás. Helyezzünk az 1001-es A csoport elejére 23 képzelt játékost, akikről tudjuk, hogy minden valódi játékosnál erősebb matadorok, és egymás közti sorrendjük is ismert, az 1000-es B-csoport végére pedig 24 dilettánst, aki minden valódi játékosnál és a 23 matadornál gyengébb, és egymás közti sorrendjük is adott. (A kitalált emberek esetleges játszmáit tehát nem kell ténylegesen lejátszani, azok kimenetelét előre tudjuk.) A 23 matadort is beleszámítva, ebben a helyzetben az összesített sorrend 1024-edik emberét kell megkeresnünk.
Vizsgáljuk általánosan azt a kérdést, hogy két 2L létszámú csapatból, amelyekben külön‐külön ismerjük az erőviszonyokat, hogyan választhatjuk ki, hogy ki van az összesített lista 2L-edik helyén. Kényelmesebb lesz most a leggyengébbtől kezdve sorszámozni rangsorban az egyes csapatok tagjait, a leggyengébbnek adva az 1-es számot.
Olyan helyzeteket fogunk létrehozni, amelyekben valamilyen n-re an jobb, mint b2L-n és an-2k gyengébb, mint b2L-n+2k. (L≥k≥0). Egy ilyen helyzetben mérkőzzék meg an-2k-1 és b2L-n+2k-1. Ha az előbbi nyer, akkor legyen n'=n-2k-1, ha az utóbbi, akkor n'=n. Ekkor világos, hogy a kiindulási helyzetet kaptuk vissza n és k helyett n'-vel és k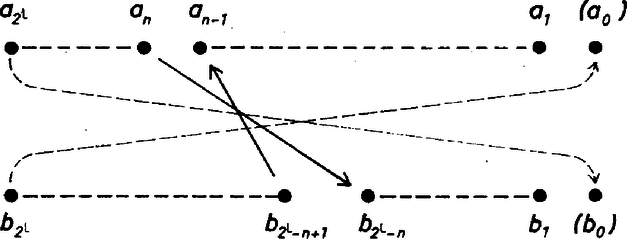-1-gyel.
 

11. ábra
 

A kezdeti helyzetet is felfoghatjuk ilyennek, ha csapatunk legelejére odaképzelünk egy a0, ill. b0 versenyzőt, akik minden eddigi teniszezőnél rosszabbak. Ekkor n=k=2L-lel fennáll, hogy a2L erősebb b0=b2L-2L-nél és a2L-2L=a0 gyengébb b2L-2L+2L=b2L-nél. (Ehhez nincs szükség tényleges játékra.) Ebből a helyzetből kiindulva az L-edik lépés után ott fogunk tartani, hogy valamilyen n-re an jobb, mint b2L-n és an-1 gyengébb, mint b2L-n+1, (11. ábra). Ekkor utolsó mérkőzésre álljon ki a két győztes: an és b2L-n+1. Mindketten erősebbek A-ból n-1 játékosnál, B-ből 2L-n-nél, összesen 2L-1-nél. A vesztes az összes többinél gyengébb, így ő a keresett játékos.
A kérdés eldöntéséhez L+1 játszma elég volt. Esetünkben a (kipótolt) csapatok létszáma 1024=210, így 11 lépésben vezet célra eljárásunk. (Vagy kevesebb lépésben, ha közben képzelt emberek játszmájára is sor kerül.)
 

Megjegyzés. Beláthatjuk, hogy a tárgyalt speciális esetek: egyenlő vagy majdnem egyenlő két csoportból a középső megkeresése, csak látszólag speciális, az általános visszavezethető erre. Legyen az A csoport m tagú, a B csoport n-tagú és keressük a versenyzők összesített rangsorában a k-adik versenyzőt (1≤k≤m+n). Legyen az elejéről k-adik versenyző a rangsor végétől számított k'-edik, ekkor k+k'=m+n+1, (12. ábra) tehát a kisebbikük ‐ vagy a közös értékük, ha egyenlők ‐ nem nagyobb, mint (m+n+1)/2. Feltehetjük, hogy k nem nagyobb ennél az értéknél, mert ellenkező esetben csak a "gyengébb'', "erősebb'', valamint a "győz'', "veszít'' szavakat (és szinonímáikat) kell felcserélni, és ezzel k és k' is szerepet cserél.
 

 

12. ábra
 

Ha k≤m≤n, akkor csak a1, ..., ak és b1, ..., bk jön tekintetbe a k-adik helyre, és így két k fős csapatból kell kiválasztani azt, aki az összesített sorrendben a két középső közül az erősebb.
Ha viszont m<k≤(m+n+1)/2, akkor
n-k≥n-m+n+12=n-m+12>0,
tehát k<n. Ekkor k<j≤n-re bj nem lehet k-adik, de nem lehet b1, ..., bk-m-1 sem, mert még ha az A csoport mind az m tagja erősebb is náluk, akkor sincs egyikük sem a k-1-edik helynél hátrább. A B csoportból tehát csak
n-(k-m-1)-(n-k)=m+1
játékost kell figyelembe venni és közülük a ranglista
k-(k-m-1)=m+1
sorszámú tagját keresni, mert a k-adik versenyzőnél biztosan jobb k-m-1 versenyzőt figyelmen kívül hagyhattunk. Ez esetben tehát egy m és egy m+1 létszámú csapatból kell a rangsorban középsőt kikeresni.
A szükséges játszmák számára a II. megoldás eljárása azt adja, hogy ha két egyenlő vagy 1-gyel különböző létszámú csapatból kell az összesített ranglistán középső, ill. a középsők közül (mondjuk) erősebb versenyzőt kiválasztani, akkor ezt L lépésben megtehetjük, ahol L azzal van meghatározva ‐ ha a versenyzők összlétszámát N-nel jelöljük ‐, hogy
2L-1<N≤2L.