| Feladat: | 1980. évi Kürschák matematikaverseny 1. feladata | Korcsoport: 18- | Nehézségi fok: nehéz |
| Megoldó(k): | Beleznay Ferenc , Bohus János , Gellér János , Horváth István , Király Zoltán , Szabó Endre , Szabó László , Tardos Gábor , Tőri Zoltán , Umann Gábor | ||
| Füzet: | 1981/február, 50 - 54. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Egyéb szinezési problémák, Térelemek és részeik, Tetraéderek, Háromszögek nevezetes tételei, Kürschák József (korábban Eötvös Loránd) | ||
| Hivatkozás(ok): | Feladatok: 1981/február: 1980. évi Kürschák matematikaverseny 1. feladata | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 1. feladat. A tér pontjait kiszínezzük színnel (mind az szín ténylegesen előfordul). Bizonyítsuk be, hogy van olyan sík, amelyik legalább különböző színű pontot tartalmaz. Megoldás. A színeket nevezzük , , , , -nek, és , , , , jelentsen a továbbiakban mindig egy‐egy , , , , ill. színű pontot. Egy egyenest, síkot, ha van rajta 3, 4, ill. 5 különböző színű pont, röviden 3-, 4-, ill. 5-színűnek fogunk nevezni. A megoldásokban gyakran fogunk használni két okoskodást, ezeket segédtételként előrebocsátjuk. 1. SEGÉDTÉTEL. Ha a feladat feltételei teljesülnek, és van egy -színű egyenes, akkor van a térben -színű sík. Valóban legyen a egyenesen mondjuk , és színű pont is. Feltétel szerint van a térben színű pont; van továbbá olyan sík, amely tartalmazza -t és -t is, egy ilyen sík pedig (legalább) 4-színű. 2. SEGÉDTÉTEL. Ha a feladat feltételei teljesülnek, továbbá egy -színű síknak és egy olyan egyenesnek, amelyiken van a maradó színű pont, van közös pontja, akkor van a térben -színű sík. Bizonyítás: Legyen az síkon , és színű pont, a egyenesen és színű pont és legyen a sík és az egyenes közös pontja. Ha színe , vagy , akkor 3-színű, és így az 1. segédtétel szerint igaz az állítás; ha pedig vagy színű, akkor 4-színű. I. megoldás. Ha , , , , közül valamelyik négyen át fektethető sík, akkor igaz a feladat állítása. Ha nem, akkor tekintsük az tetraéder oldallapjainak a síkját. Ha valamelyiknek, pl. a , , pontokat tartalmazó síknak ellenkező oldalára esik a tetraéder és , akkor metszi -t (1/a ábra). 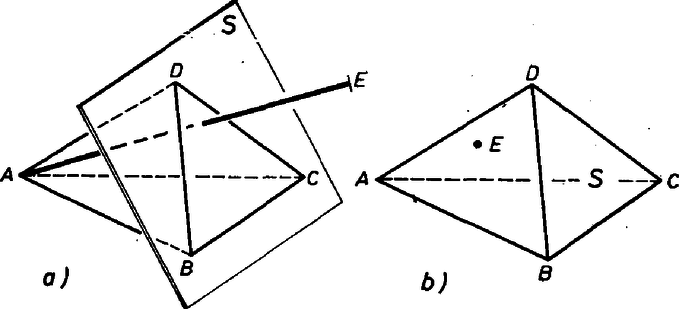 1. ábra Ha viszont bármelyik síkot véve, annak ugyanarra az oldalára esik a tetraéder és , akkor a tetraéder tartalmazza -t (1/b ábra). különbözik -tól, mert más színű, így közelebb van -hez, mint , tehát ez esetben is metszi az síkot. Ekkor azonban a 2. segédtétel értelmében igaz a feladat állítása. II. megoldás. Az , , -t tartalmazó és , , -t tartalmazó síknak van m metszésvonala, ha nem esnek egybe, mert van közös pontjuk, . Ha a két sík egybeesik, akkor az 5-színű. Ha különbözők és tartalmaz vagy színű pontot, akkor , ha pedig vagy színű pontot, akkor 4-színű. 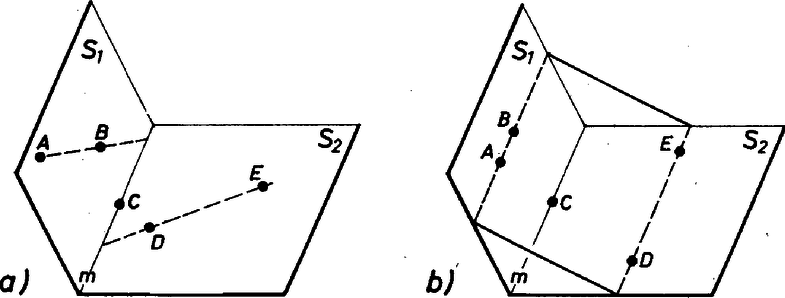 2. ábra Ha minden pontja -színű, és vagy metszi -et (2/a ábra), akkor a metsző egyenes 3-színű, és így az 1. segédtétel szerint igaz a feladat állítása. Ha végül sem, sem metszi -et, akkor mindkettő párhuzamos -mel (2/b ábra), mert -t és -et az , -t és -et az sík tartalmazza, s így kitérők nem lehetnek. Ekkor azonban és is párhuzamos, így fektethető rajtuk át sík, és ez 4-színű. III. megoldás. Legyen az -t, -t és -t tartalmazó sík. Ha ez 4-színű, akkor igaz a feladat állítása. Ha 3-színű, de a egyenes is 3-színű, vagy ha az egyenes metszi -et, akkor az 1., ill. a 2. segédtétel szerint igaz a feladat állítása. Ha 3-színű, 2-színű és párhuzamos -sel, akkor fektessünk síkot -n, -n és -n át. Ez -et egy -vel párhuzamos egyenesben metszi (3. ábra). 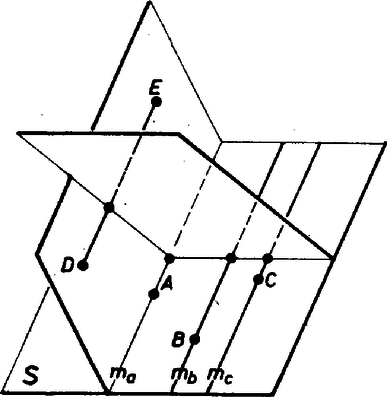 3. ábra Ha -n van vagy színű pont, akkor második síkunk 4-színű. Ha minden pontja színű és hasonlóan a -n át -vel párhuzamosan húzott egyenes színű, a -n át húzott párhuzamos pedig színű, akkor vegyünk egy -t metsző síkot. A metszéspont vagy színű, mert a egyenes 2-színű. Ez a sík metszi a párhuzamos , , egyenest is, így 4-színű. IV. megoldás. Ha van az síkot metsző, és színű ponton átmenő egyenes, akkor a 2. segédtétel szerint igaz a feladat állítása. Elég tehát azt az esetet vizsgálni, ha minden színű pont a -n átmenő, síkkal párhuzamos síkban van. Ha hasonlóan a síkot és az ponton átmenő, színű pontot is tartalmazó egyeneseket vizsgáljuk, akkor tovább szűkíthetjük a megvizsgálandó eseteket arra, hogy az színű pontok legyenek rajta az -n átmenő, síkkal párhuzamos síkon is. Hasonlóan folytatva tovább, megkívánhatjuk azt is, hogy a -n átmenő, síkkal párhuzamos síkon is, valamint a -n átmenő, síkkal párhuzamos síkon is legyenek rajta az színű pontok. 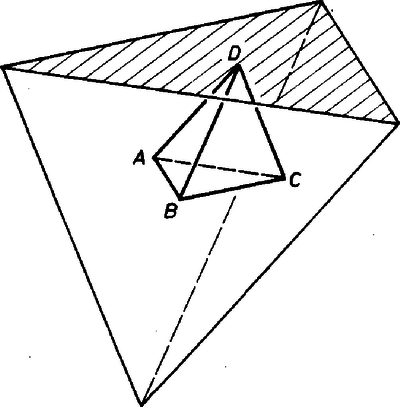 4. ábra Ez a 4 sík azonban (az tetraéderhez hasonló) tetraédert határoz meg (4. ábra), így nincs olyan pont, amelyik mindegyiken rajta lenne. Nem maradt tehát külön megvizsgálandó eset, s így mindig teljesül a feladat állítása. Eddig különböző színű pontokból indultunk ki. A következő megoldás éppen egyező színűeket keres. V. megoldás. Kell lennie a térben 3 nem egy egyenesen levő, azonos színű pontnak, hiszen különben az egész térnek nem lehetne több, mint 5 egyenese. Legyenek az háromszög csúcsai színűek. Ha minden más színű pont a háromszög síkjában van, akkor ez a sík 5-színű. Ha nem, akkor legyen a síkon kívül egy -tól különböző ‐ mondjuk színű ‐ pont . A , , egyenesek nincsenek egy síkban (5. ábra), tehát minden sík metsz legalább egy egyenest közölük. 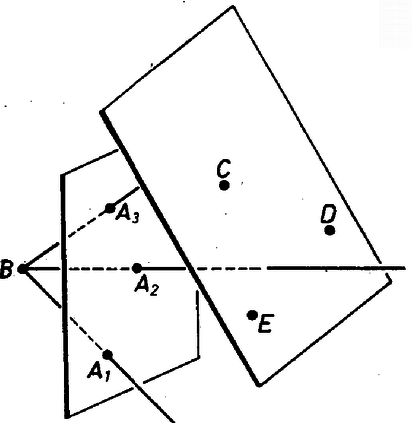 5. ábra Egy‐egy , és színű pontot véve, az ezeket tartalmazó sík tehát metszi a 3 egyenes valamelyikét, s így 2. segédtételünk alapján következik, hogy igaz a feladat állítása. VI. megoldás. Megmutatjuk, hogy ha a tér pontjai úgy vannak megszínezve, hogy egy‐egy sík legfeljebb 3-színű, akkor a tér legfeljebb 4-színű. Megjegyezzük, hogy a feltételből következik, hogy a tér minden egyenese 2-színű, hiszen ha volna 3-színű egyenes, akkor a 2. segédtétel szerint volna 4-színű sík is. Ha 4 szín sem fordul elő, akkor nyilvánvalóan igaz az állításunk. Ha , , , színe , , , ill. , akkor a 4 pont tetraédert határoz meg, hiszen nincs 4-színű sík. Legyen a tér tetszés szerinti pontja. Ha az vagy a egyenesen van, akkor az előrebocsátott megjegyzés szerint csak vagy színű, illetőleg csak vagy színű lehet. Ha egyik egyenesen sincs rajta, akkor a -n, -n és -n átmenő sík és a -n, -n és -n átmenő sík egyértelműen meg van határozva. Valamelyik síkot metszi a másikban levő tetraéderél egyenese, mert és kitérő, így mindegyiken át csak egy a másikkal párhuzamos sík fektethető, és az így keletkező két sík párhuzamos. -nek és -nek azonban közös pontja , így nem lehetnek párhuzamosak (6. ábra). 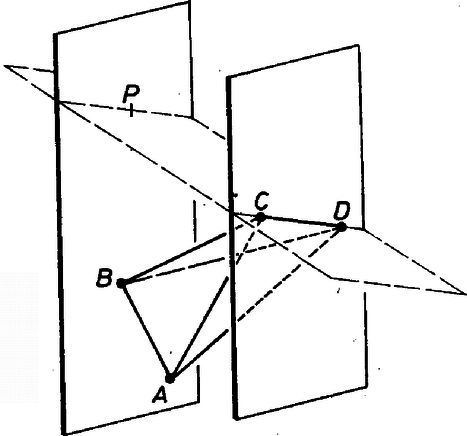 6. ábra Ha pl. metszi -t, a metszéspont vagy színű; a sík tartalmaz még és színű pontot, így színe is csak e 3 pont valamelyikével lehet egyező, mert is 3-színű. Nem fordulhat elő a tér pontjainak színe közt , , és -től különböző. A bizonyított tételből következik, hogy ha a tér több, mint 4-színű, akkor van több, mint 3-színű sík, ez pedig éppen a bizonyítandó állítás. Megjegyzések. 1. Volt, aki megmutatta, hogy 4-színű térnek nem feltétlenül van 4-színű síkja ‐ ami várható is ‐. A térben egyetlen egyenes pontjai legyenek és színűek, egy -n átmenő sík -n nem levő pontjai színűek és a tér -en nem levő pontjai színűek (7. ábra). 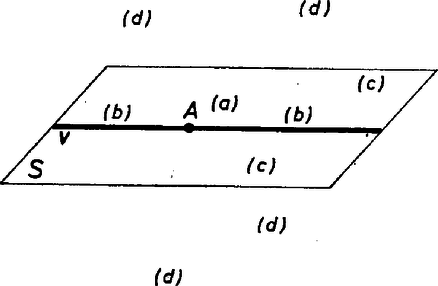 7. ábra Itt csak a sem -sel sem -vel nem párhuzamos síkok lehetnének 4-színűek, ezek azonban -et színű és vagy színű vagy színű pontokban metszik, de egyszerre mindhárom színűeket nem tartalmaznak. 2. Igaz és könnyen igazolható a feladat és az 1. megjegyzés állításának a síkbeli megfelelője: Ha egy sík pontjai 4 színnel vannak kiszínezve, akkor van olyan egyenes a síkban, amelyen előfordul 3 különböző színű pont. Ha viszont a sík minden egyenese 2-színű, akkor a sík legfeljebb 3-színű. Ezzel kapcsolatban felmerül a kérdés, hogy ha a sík pontjai csak 3 színnel vannak kiszínezve, de úgy, hogy minden színnel van színezve 3 nem egy egyenesen levő pont, vajon ebből nem kövekezik-e már 3-színű egyenes létezése. Meglepő, de A. W. Hales és E. Straus megmutatta, hogy ez nem következik. Ők megadtak olyan eljárást, amelynek segítségével úgy rendelhető a sík minden pontjához 3 szín valamelyike, hogy minden egyenes legfeljebb 2-színű legyen, de minden színhez legyen olyan háromszög, amelyiknek mindhárom csúcsa a megadott színű. Az eljárás túl bonyolult ahhoz, hogy itt ismertetni lehetne, csak azt említem meg érdekesség kedvéért, hogy kombinatorikus és számelméleti jellegű segédeszközök igen szellemes összekapcsolásával sikerül megadniuk egy kívánt tulajdonságú színezést. 3. Az egyik versenyző azt az érdekes kérdést vetette fel, hogy ha olyan 4-színű síkot keresünk, amelyiken egy előre kiválasztott szín előfordul, van-e ilyen is? Ő úgy látta, hogy nem föltétlenül található, de az általa megadott példa hibás, semmi nem derül ki belőle. A helyes válasz igenlő, hiszen van 4-színű sík a feladat állítása szerint és éppen említettük, hogy ezen van 3-színű egyenes. Legyen -n , és színű pont és legyen és , ill. színű. Ekkor bármelyik színhez jó a -t és -t vagy a -t és -t tartalmazó sík. Síkban nem ez a helyzet. Legyenek egy egyenes pontjai , , színnel színezve, a sík többi pontjai pedig színűek. Ekkor az egyetlen 3-színű egyenes, színt tartalmazó 3-színű egyenes tehát nincs. Ha most folytatjuk a színezést a térre úgy, hogy a térnek az adott síkon kívüli pontjai mind legyenek színűek, akkor csak a -n átmenő síkok négyszínűek a térben. Így nincs olyan négyszínű sík a térben, amin és szín is szerepelne. Ha tehát egy szín helyett színpárra ismételjük meg kérdésünket, akkor már a térben is tagadó a válasz. |