| Feladat: | 1979. évi Kürschák matematikaverseny 3. feladata | Korcsoport: 18- | Nehézségi fok: nehéz |
| Megoldó(k): | Beleznay Ferenc , Bohus Géza , Hajnal Péter , Szegedy Márió , Szegedy Patrik , Tardos Gábor , Varga Tamás | ||
| Füzet: | 1980/február, 56 - 57. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Kombinatorika, Gráfelmélet, Hamilton-út, -kör, Gráfok összefüggősége, Logikai feladatok, Kombinatorikai leszámolási problémák, Kürschák József (korábban Eötvös Loránd) | ||
| Hivatkozás(ok): | Feladatok: 1980/február: 1979. évi Kürschák matematikaverseny 3. feladata | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. Indirekt úton bizonyítjuk az állítást. Ha a feladat állítása nem volna igaz, akkor minden oszlophoz tartoznék legalább két olyan sor, amelyik csak a kérdéses oszlopbeli betűben különbözik. Minden oszlophoz válasszunk ki egy ilyen sorpárt. Ezt a kiválasztást szemléltethetjük úgy, hogy az -edik sort egy ponttal ábrázoljuk, és ha az -edik és -edik sor egy kiválasztott sorpár, akkor az és pontot összekötjük egy vonallal (7. ábra). Ezeket a vonalakat élnek fogjuk nevezni, az egész ábrát pedig gráfnak. Gráfunknak pontja van és ugyanannyi éle. Egy ilyen gráfban mindig van kör, vagyis olyan, különböző pontokból álló sorozat, amelyben -t -gyel és -t -gyel él köti össze. Ha ugyanis egy -pontú gráfban nincs kör, akkor annak legfeljebb pontja lehet. Ezt a megoldás a végén bizonyítjuk. 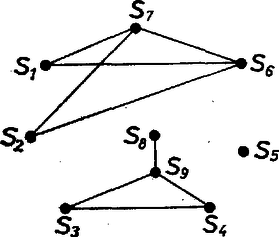 7. ábra A fenti kör a táblázatra vonatkozóan azt jelenti, hogy az -edik és -edik sor csak egy betűben, mondjuk a -edik oszlopbeliben különbözik, az előbbiben itt egy , az utóbbiban egy ettől különböző betű áll. Az -edik és -adik sor is csak egy betűben különbözik, és ezek egy másik oszlopban állnak, tehát az -adik sor -edik betűje szintén . Hasonlóan az -edik, , -adik sor -edik betűje is , de az -adik és -edik sor is csak egy betűben tér el, és ezek is egy, a -ediktől különböző oszlopban állnak, így az -edik sor -edik betűje is kellene, hogy legyen, holott ott az -től különböző betű áll. Abból a feltevésből tehát, hogy bármelyik oszlop elhagyásával keletkezik két egyező sor, ellentmondásra jutottunk. Így kell olyan oszlopnak lennie, amelyet elhagyva továbbra is minden sor különböző lesz. Egy -pontú gráf egy vagy több összefüggő részből áll, vagyis olyanból, amelyiknek bármelyik pontjából el lehet jutni az összes többibe* (7. ábra). Ha egy összefüggő gráfnak pontja van és nincs benne kör, akkor éle van. Gondoljuk a gráfot egy gátrendszer térképének. Minden pontban őrház van egy gátőrrel. Az egyik őrházban van a főőr, aki a többit irányítja (8. ábra). Nyilván minden őr el tud jutni a főőrhöz gátak mentén és csak egyféleképpen, hiszen ha volna két különböző útja is, akkor volna kör is (9. ábra). A főőr kiadja az utasítást (pl. telefonon), hogy mindenki vizsgálja meg a tőle a főőr felé vezető irányban a következő őrházig terjedő gátrészt és jelentse neki, mit tapasztalt. Ő az őrhelyén várja a jelentéseket.  8. ábra  9. ábra Ekkor egy szakaszt sem vizsgálnak ketten, mert ha ketten vizsgálnák, akkor az egyikük a megszokott útja helyett úgy is eljuthatna a főőrhöz, hogy a kérdéses szakaszra nem lép, hanem az azon feléjövő társát bevárva annak az útját követné (10/ ábra). Minden gátszakaszt megnéz valaki, mert ha az egyik végén lakó őr a szakasz érintése nélkül jut el a főőrhöz (vagy ő maga a főőr), akkor a másik végén lakó őr útja csak az lehet, hogy végigmegy a kérdéses szakaszon és utána a szomszédos őr útját követi (10/ ábra). Eszerint őr minden szakaszt megvizsgál és mindegyiket csak egy gátőr, tehát gátszakasz van, vagyis a gráfban él. Ezzel bebizonyítottuk az állítást. Ha egy szögpontú, kört nem tartalmazó gráf több összefüggő részre bomlik, akkor mindegyik részben eggyel kevesebb él van, mint pont, így a gráfnak -nél kevesebb éle van. 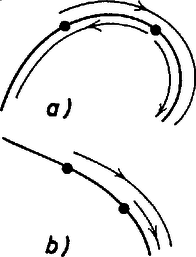 10. ábra Két sor esetén van legalább két oszlop és van köztük olyan, amelyikben a két sorban különböző betűk állnak. Bármelyik további oszlopot (ha több van, akár mindet együtt is) elhagyhatjuk. Tegyük most fel, hogy -nél kevesebb soros (és legalább ugyanannyi oszlopos) táblázatra igaz az állítás, és vegyünk egy soros táblázatot, amelyik kielégíti az állítás feltételeit. Hagyjuk el az első oszlopot. Ha a sorok ezután is páronként kölönbözők, akkor az állítás igaz. Ha bizonyos sorok így egyenlővé váltak, akkor az egyenlővé vált sorok közül csak egyet-egyet tartsunk meg. Így eggyel fogyott az oszlopok száma és legalább egy sort is elhagytunk, tehát továbbra is legalább annyi oszlop van, mint sor, továbbá bármely két sor különböző. Erre a táblázatra feltevés szerint igaz az állítás: elhagyható egy oszlop úgy, hogy a sorok mind különbözők maradjanak. Hagyjuk el a megfelelő oszlopot az eredeti táblázatból és nézzünk két sort. Ha mindkettő szerepelt a megritkított táblázatban is, akkor különbözők már akkor is, ha még az első betűket is figyelmen kívül hagyjuk. Ha viszont egy olyan csoportban vannak, amiből csak egy sor került a megritkított táblázatba, akkor az első betűk különbözők. Ekkor is találtunk tehát olyan oszlopot, amelyiknek az elhagyása után bármely két sor különböző maradt. A tulajdonság tehát öröklődik az -soros táblázatokra is. 2. Sokan az ábécé betűinek a számából próbáltak következtetni. Ez zsákutca volt, hiszen már két jellel is ki lehet tölteni a táblázatot a feltételeknek megfelelően. Egy ilyen kitöltést kapunk, ha az előző megjegyzés táblázatát egy csupa -ból álló oszloppal egészítjük ki. *Egy-egy ilyen rész állhat egyetlen pontból is. |