Kezdőlap


Feladat:	1979. évi Kürschák matematikaverseny 1. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Beleznay Ferenc , Bohus Géza , Hajnal Péter , Szegedy Márió , Szegedy Patrik , Tardos Gábor , Varga Tamás
Füzet:	1980/február, 52 - 54. oldal		PDF \| MathML
Témakör(ök):	Gúlák, Szabályos sokszög alapú gúlák, Maradékos osztás, Szabályos sokszögek geometriája, Gömbi geometria, Köréírt gömb, Alakzatok köré írt kör, Húrsokszögek, Egyenlő szárú háromszögek geometriája, Háromszögek egybevágósága, Középpontos tükrözés, Kör geometriája, Vetítések, Téglalapok, Síkra vonatkozó tükrözés, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):	Feladatok: 1980/február: 1979. évi Kürschák matematikaverseny 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a gúla alapja az $A_{1} A_{2} ... A_{n}$ sokszög ( $n$ páratlan egész szám), az alaplappal szemközti csúcs $B$ . Feltétel szerint $A_{1}, A_{2}, ..., A_{n}$ egyenlő távol van $B$ -től, tehát egy $B$ középpontú gömbön helyezkedik el; továbbá az alaplap síkjában is van, tehát rajta van a két felület metszésvonalán, egy körön. Az alaplap tehát húrsokszög.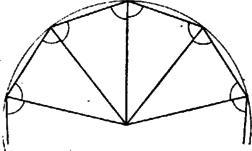
Elég megmutatni, hogy a sokszög oldalai egyenlők. Valóban, ha ez igaz, akkor összekötve minden csúcsot a körülírt kör középpontjával, egybevágó egyenlő szárú háromszögekre bontjuk a sokszöget (1. ábra). Ebből következik, hogy a sokszög szögei is egyenlők (a háromszögek száraival szemközti szög kétszerese mindegyik).

1. ábra

Azt mutatjuk meg, hogy az alaplap második szomszéd oldalai egyenlők. Páratlan oldalú sokszög esetén ebből következik, hogy minden oldal egyenlő, mivel minden oldalról a második szomszédjára térve át páratlan oldalszám esetén bejárjuk az összes oldalt.
Tekintsük az

A_{i} A_{i + 1}

élt felező, rá merőleges

S

síkot. Ez az

A_{i}

-től és

A_{i + 1}

-től egyenlő távolságra levő pontok halmaza. Mivel

B A_{i} = B A_{i + 1}

, így

S

átmegy

B

-n (2. ábra). Ha tükrözünk

S

-re,

A_{i}

és

A_{i + 1}

helyet cserél, az alaplap síkja pedig önmagába megy át, mivel a sík merőleges

S

-re. Ugyancsak önmagukba mennek át a

B

középpontú gömbök is. Ezért önmagába megy át a tükrözéskor az alaplap köré írt kör is.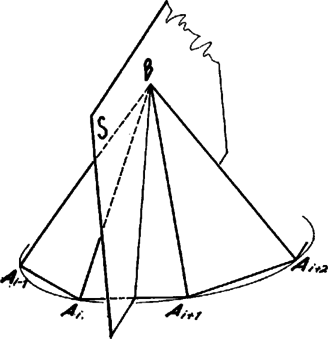

2. ábra

Megmutatjuk, hogy az

A_{i - 1}

csúcs¹ tükörképe

A_{i + 2}

. Jelöljük

A_{i - 1}

tükörképét

C

-vel. Ez is a körülírt körön van. A tükrözés folytán az

A_{i - 1} A_{i} B

és

A_{i} A_{i + 1} B

lapok szöge megegyezik a

C A_{i + 1} B

és

A_{i + 1} A_{i} B

lapok szögével. A gúla konvex volta miatt

A_{i - 1}

A_{i + 2}

és

C

A_{i} A_{i + 1} B

síknak ugyanazon az oldalán fekszik. De az

A_{i + 1} B

egyenes határolta, azt tartalmazó félsíkhoz a határegyenese mentén csak egy olyan félsík illeszthető, amelyik vele adott szöget zár be és az

A_{i} A_{i + 1} B

sík megadott oldalán fekszik (3. ábra). Így

C

és

A_{i + 2}

egy síkban fekszik, rajta van egy nem ebben a síkban levő körön és különbözik a sík és kör

A_{i + 1}

metszéspontjától, tehát kell, hogy egybeessenek.

A_{i - 1} A_{i}

és

A_{i + 1} A_{i + 2}

tehát egymás tükörképei, és így egyenlők. Ez igaz

i = 1,2, ..., n

-re, vagyis az alaplap mindegyik oldala egyenlő a rá következő másodikkal. Mint láttuk, ebből következik, hogy az alap szabályos sokszög.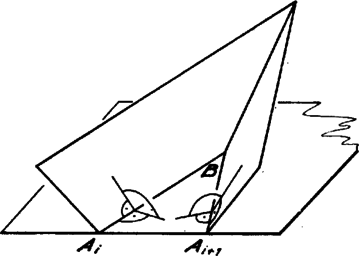

3. ábra

Megjegyzések. 1. Az oldalélek egyenlőségéből már következik a gúla konvex volta, pl. a következők alapján: ha nem volna konvex a gúla, ez azt jelentené, hogy van olyan

P

és

Q

belső pontja, amelyeket összekötő szakasznak van pontja a gúlán kívül. Vetítsük a

P Q

szakaszt az alappal szemközti csúcsból az alap síkjára. A

P' Q'

vetület olyan szakasz volna (4. ábra), amelynek végpontjai az alaplap belsejében vannak, de van az alaplapon kívül levő pontja. Így az alaplap konkáv sokszög volna.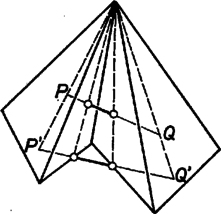

4. ábra

Húrsokszög viszont nem lehet konkáv, hiszen akkor volna a belső szögei közt

180^{\circ}

-nál nagyobb. Annak csúcsa körül elég kis sugarú kört rajzolva ennek a szögtartományba eső (konkáv) körcikke a sokszög belsejében volna (5. ábra). De ennek a körcikknek volna a sokszög köré írt körön kívül eső pontja, márpedig egy húrnégyszögnek nincs a körön kívüli pontja.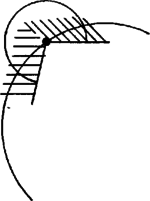

5. ábra

Egy ilyen jellegű bizonyítással azonban nem kívánta a szervező bizottság megterhelni a versenyzők rendelkezésére álló időt.
2. Többen rámutattak, hogy páros oldalszámú gúlára nem feltétlenül teljesül a feladat állítása. A legegyszerűbb ellenpélda erre egy téglalap alapú ,,egyenes'' gúla. Az alappal szemközti csúcs merőleges vetülete a téglalap középpontja. Általában tekintsük egy

O

középpontú körbe írt

2 n

oldalú szabályos sokszöget,

(n \geq 2)

és távolítsuk minden második oldalát ugyanannyival a középponttól, majd a szomszédos végpontokat kössük össze (6. ábra). Könnyű látni, hogy az így keletkezett

2 n

-szög szögei is egyenlők. Összekötjük a sokszög csúcsait az

O

pontban a sokszög síkjára emelt merőleges egy

P

pontjával. A keletkezett gúla szomszédos lapjai egyenlő szöget zárnak be, amint az az alapélek felezőpontjában állított, az élre merőleges síkra történő tükrözéssel belátható. A gúla alapja azonban nem szabályos sokszög.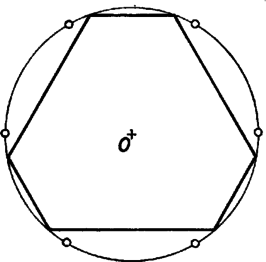

6. ábra

¹Ha

i = n

A_{i + 1}

-en

A_{1}

értendő,

A_{i + 2}

-n

A_{2}

i = 1

esetén pedig

A_{i - 1}

-en

A_{n}