| Feladat: | 1977. évi Kürschák matematikaverseny 3. feladata | Korcsoport: 18- | Nehézségi fok: nehéz |
| Megoldó(k): | Cseri István , Knébel István , Kozma László , Pyber László , Spissich László , Surány Gábor , Zádori László , Zempléni András | ||
| Füzet: | 1978/február, 55 - 57. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Kombinatorika, Kombinatorikai leszámolási problémák, Teljes indukció módszere, Maradékos osztás, Kürschák József (korábban Eötvös Loránd) | ||
| Hivatkozás(ok): | Feladatok: 1978/február: 1977. évi Kürschák matematikaverseny 3. feladata | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. Megkérdezünk mindenkit, hány ismerőse van egy-egy iskolában. Legyen a legkisebb hallott szám . Ez nem , mert mindenkinek több ismerőse van a másik két iskolából, mint ahány tanuló jár egy-egy iskolába. Nem vezethetjük vissza a módosított állítást az eredetire úgy, hogy egyes ismeretségeket figyelmen kívül hagyunk. Lehetséges ugyanis, hogy Andrásnak pl. több mint ismerőse van a másik két iskolában, azonban mindegyik ismerőse csak tanulót ismer a másik két iskolából. Ekkor András bármelyik ismeretségét figyelmen kívül hagyva, volt ismerősének már csak ismerőse marad a másik két iskolában. Ha minden tanuló a másik két iskolában együtt legalább tanulót ismer, akkor kiválasztható mindegyik iskolából egy-egy tanuló úgy, hogy mindegyikük ismerje a másik kettőt. A bizonyítást teljes indukcióval végezzük. Ha történetesen mindegyik iskolának csak 1‐1 tanulója van, akkor a feltétel éppen azt kívánja, hogy mindegyikük ismerje a másik kettőt. Legyen most és tegyük fel, hogy minden természetes számra igaz az állítás, ha az iskolákba gyerek jár. Legyen továbbá , és három iskola, amelyek mindegyikébe tanuló jár és mindegyikük legalább tanulót ismer a másik két iskolából. Az iskola tanulója ismerje a iskolából -et, ő a iskolából -et. Ha ismeri -et, akkor ő hármukra teljesül a feladat állítása. Ha nem, akkor egy -beli ismerőse legyen és folytassuk az eljárást mindig ugyanebben a sorrendben véve az iskolákat, míg egy olyan tanulóhoz nem érünk, aki egyszer már szerepelt a felsorolt ismerősök közt. Ez a tanuló és az utána felsoroltak egy olyan kört alkotnak, amelyben mindenki ismeri a szomszédait és amelyikhez mindegyik iskolának ugyanannyi tanulója tartozik. Legyen ez a szám . Ha , ez azt jelenti, hogy teljesül a feladat állítása. Ha (a kör tartalmazza az összes tanulót), akkor válasszunk ki egy tanulót, pl. az -beli -et. A körben szomszédos és -beli tanulók párt alkotnak, amelyek , , tanulói ismerik egymást. (A 6. ábra a tanulókat ponttal, az ismeretséget összekötéssel szemlélteti.) 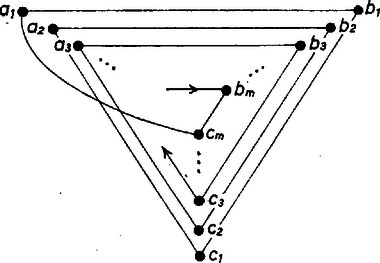 6. ábra Mivel -nek a két iskolában legalább ismerőse van, így legalább egy pár mindkét tagját ismeri. Ekkor azonban erre a tanulóra teljesül a feladat állítása. Ha , akkor nézzük az iskoláknak a körhöz nem tartozó tanulóit. Minden iskolában -an vannak. Ha mindegyiküknek legalább ismerőse van a másik két iskola megmaradt tanulói közt, akkor az indukciós feltétel szerint kiválasztható a feladat állítását kielégítő három tanuló. Ha pl. az iskolabeli -nek a és iskolában megmaradt tanulók közt legfeljebb ismerőse van, akkor a körnek legalább -be és -be járó tanulóját ismeri. Ezeket azonban a kör most darab ismerősökből álló párba sorolja, s így ismer legalább egy ilyen párt. Minden esetben találtunk tehát a feladat állítását kielégítő hármast. Ezzel az indukciós bizonyítást befejeztük. 2. Nyilvánvalóan nem elég, ha csak annyit teszünk fel, hogy minden tanulónak ismerőse van a másik két iskolában. Legyen minden iskolában páros számú tanuló, mondjuk mindegyikben fiú és lány. Ha az iskola lányai ismerik a iskolából a lányokat, a -ből a fiúkat, az -ba járó fiúk a -ből a fiúkat, a -ből a lányokat, továbbá a -ből és -ből a lányok a lányokat, a fiúk a fiúkat, akkor mindenkinek annyi ismerőse van, ahány gyerek egy-egy iskolába jár, de nincs a feladat követelményeit kielégítő három tanuló. Ha az egy-egy iskolába járó tanulók száma páratlan, akkor nem is lehet mindenkinek pontosan annyi ismerőse, ahányan egy iskolába járnak, hiszen akkor mindenkit megkérdezve ismerősei számáról, minden ismeretséget kétszer vennénk számba, viszont páratlan számú tanuló mindegyike páratlan számú ismerőst említene, ami együtt ismét páratlan számot adna. 3. Felmerülhet az a kérdés is, hogy megvalósítható-e tetszés szerinti tanulószám mellett a feladat eredeti feltétele. A válasz igenlő. Egy lehetőség a megvalósításra a következő. Ha páratlan számú tanuló, van iskolánként, akkor sorszámozzuk iskolánként a tanulókat. Az iskola minden tanulója ismerje a és a iskola vele egyenlő sorszámú tanulója utáni tanulót, úgy értve, hogy ha a sor végére érünk, akkor az elejéről folytatjuk. Ekkor a és a iskola minden tanulója -ból a vele egyező sorszámú tanuló előtti tanulót ismeri. Ismerje továbbá a iskola minden tanulója -ből a vele egyező sorszámú tanuló utáni tanulót. (Ekkor a -beli tanulók -ből a velük egy sorszámú tanuló előtti tanulót ismerik.) Ekkor minden tanulónak ismerőse van. Ha viszont minden iskolába tanuló jár, mondjuk fiú és lány, akkor ismerjék egymást a különböző iskolabeli lányok a különböző iskolabeli fiúkkal, továbbá az iskolabeli fiúk ismerjék a iskolából a velük egy sorszámú lányt, a -beli fiúk a -beli velük egy sorszámú lányt, és a -beli fiúk az -beli velük egy sorszámú lányt. Ekkor mindenkinek ismerőse van. Természetesen számos más lehetőség is van a feltételek megvalósítására. |