Kezdőlap


Feladat:	1977. évi Kürschák matematikaverseny 2. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Cseri István , Hajnal Péter , Knébel István , Varga Tamás
Füzet:	1978/február, 51 - 55. oldal		PDF \| MathML
Témakör(ök):	Háromszögek nevezetes tételei, Súlyvonal, Körülírt kör, Középpontos tükrözés, Húrnégyszögek, Thalesz-kör, Kör geometriája, Derékszögű háromszögek geometriája, Vetítések, Súlypont, Egyenlő szárú háromszögek geometriája, Magasságpont, Körülírt kör középpontja, Vektorok, Vektorok lineáris kombinációi, Helyvektorok, Vektorok skaláris szorzata, Magasságvonal, A komplex szám algebrai alakja, Komplex számok tulajdonságai, Rombuszok, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):	Feladatok: 1978/február: 1977. évi Kürschák matematikaverseny 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. 1. Megmutatjuk, hogy az $M$ magasságpontnak a $B C$ oldal $F_{1}$ felezőpontjára vonatkozó $M_{1}$ tükörképe az $A B C$ háromszög köré írt körön van, annak éppen az 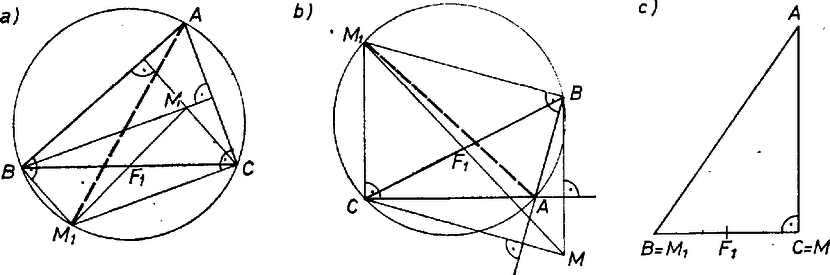$A$ -val átellenes pontja.
Ebből már könnyen fog következni a feladat állítása.
$B$ és $C$ egymás tükörképe $F_{1}$ -re. Ha $M$ különbözik a $B$ és $C$ csúcstól, akkor

\begin{matrix} M_{1} B ‖ M C és M_{1} C ‖ M B, \end{matrix}

mert pontra való tükrözés egyenest vele párhuzamos egyenesbe visz át (1

a

és

b

ábra). Azonban

M C

A B

oldalra bocsátott magasság egy szakasza,

M B

pedig az

A C

oldalra bocsátotté, így

\begin{matrix} A B M_{1} ∢ = A C M_{1} ∢ = 90^{\circ}, \end{matrix}

tehát

B

és

C

rajta van az

A M_{1}

mint átmérő fölé rajzolt körön. Az

A B C

háromszög köré rajzolt kör azonban egyértelműen meg van határozva, így azonos az

A M_{1}

átmérőjű körrel, tehát

M_{1}

a háromszög köré írt körnek

A

-val átellenes pontja, amint állítottuk.

1. ábra

Az állítás akkor is igaz, ha pl.

M = C

c

. ábra). Ez ugyanis azt jelenti, hogy

\begin{matrix} A C ⊥ B C, \end{matrix}

a háromszög derékszögű.

M

tükörképe

F_{1}

-re

B

-vel esik egybe és ez valóban az

A

-val átellenes pont.
2. A bizonyított tételből következik, hogy

A_{2}

B_{2}

és

C_{2}

M

pont merőleges vetülete a háromszög súlyvonalain. Elég ezt pl.

A_{2}

-re belátni. Ha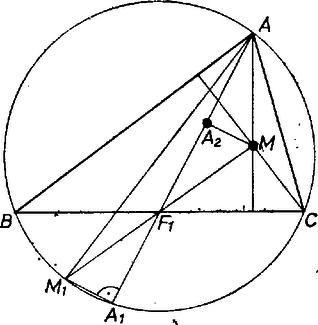

M_{1} \neq A_{1}

, akkor

\begin{matrix} F_{1} A_{1} M_{1} ∢ = A A_{1} M_{1} ∢ = 90^{\circ}, \end{matrix}

mert

A M_{1}

átmérő (2. ábra). Tükrözve

F_{1}

-re, kapjuk, hogy

\begin{matrix} F_{1} A_{2} M ∢ = 90^{\circ}, \end{matrix}

és ezt állítottuk. Ha

A_{1} = M

, akkor

A_{2} = M

, tehát ekkor is igaz az állítás.

2. ábra

Tudjuk, hogy a háromszög súlyvonalai egy ponton mennek keresztül, a háromszög

S

súlypontján. Ha

S \neq M

, akkor

A_{2}

B_{2}

és

C_{2}

S M

átmérőjű körön van. Ha

S = M

‐ ez csak a szabályos háromszögre teljesül ‐, akkor egybeesik velük

A_{2}

B_{2}

és

C_{2}

is és van végtelen sok kör, amelyik mindegyik pontot tartalmazza.
Azt bizonyítottuk tehát be, a feladat állításán túlmenve, hogy minden háromszöghöz van olyan kör, amelyik átmegy

A_{2}

-n,

B_{2}

-n,

C_{2}

-n, a háromszög magasságpontján és súlypontján.

II. megoldás. Jelöljük a háromszög köré írt kör középpontjából az

A

B

C

A_{1}

B_{1}

C_{1}

A_{2}

B_{2}

C_{2}

és

M

ponthoz mutató vektorokat rendre

a

b

c

a_{1}

b_{1}

c_{1}

a_{2}

b_{2}

c_{2},

ill.

m

-mel. Közülük az első hat hossza egyenlő, a kör sugara.
Megmutatjuk, hogy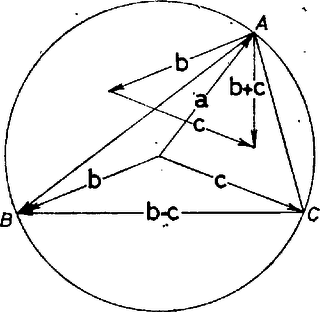

\begin{matrix} m = a + b + c . \end{matrix}

Jelöljük

N

-nel azt a pontot, amelynek a jobb oldali vektor a helyvektora (3. ábra). Ekkor

\begin{matrix} \vec{A N} = b + c, \vec{C B} = b - c . \end{matrix}

Ha ezek egyike sem

0

nulla-vektor, akkor merőlegesek, mert egy olyan rombusz átlóvektorai, amelynek az oldalvektorai felváltva

\pm b

-vel, ill.

\pm c

-vel egyenlők. Vagy mert skaláris szorzatuk:

\begin{matrix} (b + c) \cdot (b - c) = b \cdot b - c \cdot c = {| b |}^{2} - {| c |}^{2} = 0. \end{matrix}

A N

egyenes tehát a

B C

-re merőleges magasság egyenese.

3. ábra

Mivel

B

és

C

különböző pontok, így

\begin{matrix} b - c \neq 0 . \end{matrix}

b + c = 0

, akkor

N = A

, s így ekkor is rajta van

N

A

-ból húzott magasságvonalon. Ugyanígy látható, hogy

N

rajta van a másik két magasságvonalon is, tehát azonos a háromszög magasságpontjával. Ezt akartuk belátni.
Azt, hogy

A_{2}

A_{1}

tükörképe a

B C

szakasz középpontjára, a következő vektoregyenlőség fejezi ki:

\begin{matrix} \frac{1}{2} (a_{1} + a_{2}) = \frac{1}{2} (b + c) . \end{matrix}

Innen

\begin{matrix} a_{2} = b + c - a_{1} . \end{matrix}

Most már könnyen láthatjuk, hogy

\begin{matrix} M A_{2} ⊥ A A_{1}, \end{matrix}

(1)

ugyanis

\begin{matrix} {\vec{M A}}_{2} = a_{2} - m = - (a + a_{1}), {\vec{A A}}_{1} = a_{1} - a . \end{matrix}

a

és

a_{1}

egyenlő hosszú vektorok. Ebből a fentebbi meggondoláshoz hasonlóan adódik, hogy vagy

M = A_{2}

, vagy teljesül az (1) összefüggés. Ebből pedig következik a feladat állítása, amint azt az I. megoldásban láttuk.

Megjegyzés. Érdekes megoldás adódik a feladatra komplex számok segítségével. A komplex számok eközben csak arra fognak szolgálni, hogy átfogalmazzuk segítségükkel az állítást egy könnyen belátható geometriai állítássá.

A komplex számokról a következőket használjuk fel. Ugyanazok a számolási szabályok érvényesek rájuk, mint a valós számokra.
A komplex számok a sík vektoraival szemléltethetők. Ebben a szemléltetésben az összeadást a vektorösszeadás szemlélteti.
Két komplex szám hányadosát ábrázoló vektor hajlásszöge a pozitív abszcisszatengelyhez az osztó irányszögével kisebb mint az osztandó irányszöge.
A valós számokat az abszcissza-tengelyen szemléltetjük, ezek irányszöge tehát

0^{\circ}

vagy

180^{\circ}

(vagy ezektől

360^{\circ}

egy egész többszörösével különbözhet).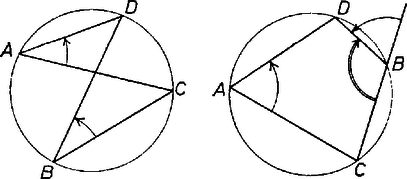

4. ábra

Legyen most már

A

B

C

D

a sík négy különböző pontja, a helyvektoraik által szemléltetett komplex számok

a

b

c

d

. Ha a négy pont egy körön van, akkor a

C A D ∢

és

C B D ∢

vagy egyenlő és egyirányú, vagy

180^{\circ}

-ra egészíti ki egymást és ellentétes irányú (4. ábra). Ugyanez áll tehát a

\begin{matrix} \frac{d - a}{c - a} és \frac{d - b}{c - b} \end{matrix}

(2)

komplex számok irányszögére is. Ez azt jelenti, hogy a

\begin{matrix} \frac{d - a}{c - a} : \frac{d - b}{c - b} = \frac{(d - a) (c - b)}{(c - a) (d - b)} \end{matrix}

(3)

hányados irányszöge

0^{\circ}

vagy

180^{\circ}

, ez a szám tehát valós. Ez akkor is igaz, ha

d = a

, vagy

c = b

. Ez azt jelenti, hogy legalább

2

pont egybeesik. Ekkor pedig a pontokon át lehet kört rajzolni, kivéve ha három egy egyenesen levő pontunk van.
Tegyük most fel, hogy a

(3)

szám

0

-tól különböző és valós. Ekkor a

(2)

alatti (komplex) számok is

0

-tól különbözők és irányszögeik vagy egyenlők vagy

180^{\circ}

-kal különböznek. Lehet mind a két szám valós, de ha egyik nem az, akkor a másik sem az.
Ha mind a kettő valós, akkor

A

C

és

D

is,

B

C

és

D

is egy egyenesen van, tehát a négy pont egy egyenesen van. Ha viszont a

(2)

számok nem valósak, akkor a szögekre nyert összefüggés éppen azt jelenti, hogy

A B C D

húrnégyszög, a négy pont egy körön van. A következőt nyertük tehát:
A

(3)

komplex szám akkor és csak akkor valós, ha

A

B

C

D

egy körön vagy egy egyenesen van. Az alábbiakban ezt fogjuk felhasználni.

III. megoldás (komplex számok felhasználásával). Válasszuk a háromszög köré írt kör középpontját a komplex számsík

0

pontjának és az

A

B

C

A_{1}

B_{1}

C_{1}

A_{2}

B_{2}

C_{2}

M

pontok ábrázolják rendre az

a

b

c

a_{1}

b_{1}

c_{1}

a_{2}

b_{2}

c_{2}

m

komplex számokat. Ekkor, mint az előző megoldásban, adódnak az

\begin{matrix} a_{2} = b + c - a_{1} b_{2} = c + a - b_{1}, c_{2} = a + b - c_{1} m = a + b + c \end{matrix}

összefüggések. Ha a négy pont egy körön van, akkor a következő komplex szám valós:

\begin{matrix} \frac{(a_{2} - c_{2}) (b_{2} - m)}{(b_{2} - c_{2}) (a_{2} - m)} = \frac{(c + c_{1} - (a + a_{1})) (- (b + b_{1}))}{(c + c_{1} - (b + b_{1})) (- (a + a_{1}))} = \frac{(a + a_{1} - (c + c_{1})) (b + b_{1})}{(b + b_{1} - (c + c_{1})) (a + a_{1})} . (4) \end{matrix}

Az utolsó tört valós volta viszont azt jelenti, hogy az

\begin{matrix} a + a_{1}, b + b_{1}, c + c_{1} és 0 \end{matrix}

komplex számokat ábrázoló pontok egy körön vagy egy egyenesen vannak. Az utolsó pont a háromszög köré írt kör középpontja.
Mivel

a

és

a_{1}

abszolút értéke (az ábrázoló vektorok hossza) egyenlő, így a

0

-t,

a

-t,

a_{1}

-et és

(a + a_{1})

-et ábrázoló pontok egy rombusz csúcsai. Ekkor azonban az

(a + a_{1})

-et ábrázoló pont az

O

pont tükörképe a rombusz másik két csúcsát összekötő egyenesre, vagyis az

A A_{1}

súlyvonal egyenesére. Jelöljük ezt

A'

-vel (5. ábra), hasonlóan a

(b + b_{1})

-et és

(c + c_{1})

-et ábrázoló

B'

és

C'

pont az

O

pont tükörképe a háromszög

B

-ből, ill.

C

-ből induló súlyvonalára.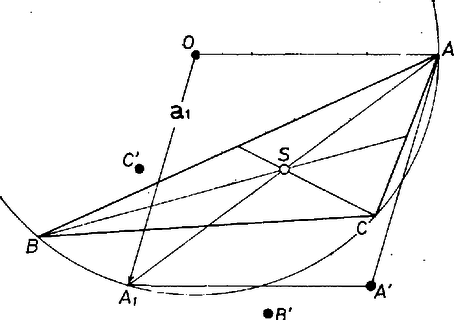

5. ábra

Nyilvánvaló azonban, hogy

O

A'

B'

C'

egy körön van, mert a három súlyvonal átmegy a háromszög

S

súlypontján. Ez a pont tehát mind a három tükrözésnél helyben marad, s így

\begin{matrix} S O = S A' = S B' = S C' . \end{matrix}

Ekkor a

(4)

tört értéke valós, viszont

\begin{matrix} \frac{a + a_{1} - (c + c_{1})}{b + b_{1} - (c + c_{1})} \end{matrix}

nem valós, mert

A'

B'

és

C'

nincs egy egyenesen. Az utolsó tört azonban éppen az

\begin{matrix} \frac{a_{2} - c_{2}}{b_{2} - c_{2}} \end{matrix}

tört, tehát ez sem valós,

A_{2}

B_{2}

C_{2}

nincs egy egyenesen. Ebben az esetben

A_{2}

B_{2}

C_{2}

és

M

-nek kell egy körön lennie, és ezt akartuk bizonyítani.