Feladat: 1976. évi Kürschák matematikaverseny 1. feladata Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Magyar Zoltán 
Füzet: 1977/február, 50 - 54. oldal  PDF  |  MathML 
Témakör(ök): Paralelogrammák, Középpontos tükrözés, Eltolás, Háromszögek nevezetes tételei, Pont körüli forgatás, Kör geometriája, Középponti és kerületi szögek, Húrnégyszögek, Tengelyes tükrözés, Rombuszok, Szimmetrikus alakzatok, Egyéb sokszögek hasonlósága, Háromszögek hasonlósága, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1977/február: 1976. évi Kürschák matematikaverseny 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Állapítsuk meg először, hol helyezkedik el a P pont. Megmutatjuk, hogy nem lehet az AB, AD félegyenesek meghatározta, C-t tartalmazó szögtartományban. Valóban, az itt fekvő P pontokra* a PAB∢ része a DAB∢-nek, a PCB∢ viszont tartalmazza a DAB∢-gel egyenlő DCB∢-et.

 
 

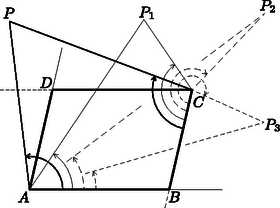1. ábra
 

Hasonlóan nem lehet P az A-t tartalmazó DCB szögtartományban sem, tehát vagy az AB és CB egyenesek B-n túli meghosszabításai közti kenvex szögtartományban van, vagy AD-nek és CD-nek a D-n túli meghosszabításai közt.
Feltehetjük, hogy az előbbiben, mert ellenkező esetben az ellentétesen irányított BAP és BCP szögekkel együtt a paralelogramma A-nál, ill. C-nél levő szögével csökkentett DAP és DCP szögek nagysága is egyenlő és irányításuk ellentétes. Így tükrözve a paralelogramma középpontjára, visszavezettük a problémát arra az esetre, amikor P az AB és CB meghosszabbítása határolta tartományban van.
Toljuk el a P pontot a BC vektorral. Új helyzete legyen P1 (2. ábra). Ekkor a DCP1 háromszög az ABP háromszög eltolt képe, BPP1C pedig paralelogramma. A P1DC∢ és a PAB∢ irányítás és nagyság szerint megegyezik. Utóbbi a feladat feltétele szerint a BCP∢-gel egyezik meg nagyságban és irányításra is, ez pedig a P1PC∢-gel, mert a BPP1C paralelogramma középpontjára való tükrözés egymásba viszi át a kettőt.
 
 

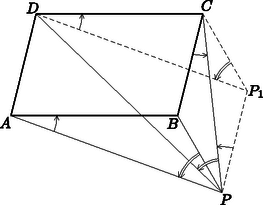2. ábra
 

Azt nyertük tehát, hogy a P-t és a D-t P1-gyel összekötő egyenest egyező irányban egyenlő szöggel elfordítva kapjuk a C-n átmenő egyeneseket. Ez azonban azt is jelenti, hogy C, D, P és P1 egy körön van. Ekkor a P-t és P1-et C-vel összekötő egyeneseket is egyező irányú és nagyságú forgás viszi át a P-t ill. P1-et, D-vel összekötő egyenesekbe. A P1C, P1D egyeneseket viszont CB vektorral eltolva a PB, PD egyeneseket kapjuk. Az előbbit az utóbbiba tehát ugyanolyan irányú és nagyságú forgás viszi át, mint PC-t PD-be. Ezzel a feladat állítását bebizonyítottuk.
 
Megjegyzések. 1. A kerületi szögek tételét nem egészen megszokott formában fogalmaztuk meg. Ezt azért tettük, mert ebben a formában szükséges és elégséges feltételét kapjuk annak, hogy négy pont egy körön feküdjék, anélkül, hogy vizsgálni kellene a pontok egymáshoz viszonyított elhelyezkedését a síkban.
Az A, B, U, V pontok akkor és csak akkor vannak egy körön, ha az AU és BU egyenest ugyanolyan nagyságú és irányú elforgatás viszi át az AV, ill. BV egyenesbe (3. ábra).
 
 

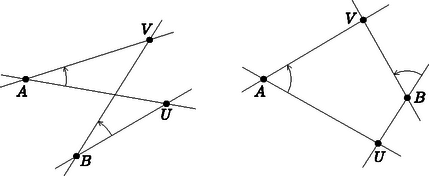3. ábra
 

A tétel ilyen megfogalmazását használva elhagyhatjuk azt a feltevést is, hogy a P pont a paralelogrammán kívül van. Minden esetben igaz, hogy ha a feladat további feltételei teljesülnek, akkor a P-t B-vel, ill. C-vel összekötő egyenes egyező nagyságú szöggel forgatható egyező irányban az A-val, ill. D-vel összekötő egyenesbe. A fenti bizonyítás változtatás nélkül érvényes marad, amint az a 4. ábrán könnyen követhető.
 
 

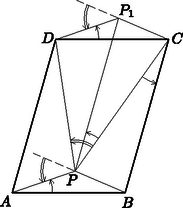4. ábra
 

2. Az előző megjegyzésben megfogalmazott tételt, illetőleg annak megfelelő összefüggéseket általában a középponti és kerületi szögek közti összefüggésből szokás levezetni, a tétel azonban könnyen belátható közvetlenül is.
 
Először kissé módosítjuk a kerületi szög és a belefoglalt körív fogalmát. Kerületi szögnek nevezzük két egyenes szögét, ha az egyenesek a kör kerületén metszik egymást. Tekintsük az egyenesek másik metszéspontját a körrel. A két egyenes szöge által befoglalt köríven a körnek a metszéspontok közti két íve közül azt értjük, amelyiket a két egyenes adott nyílásszögű szögtartománya tartalmaz. Ha az egyenesek irányított szögét tekintjük, akkor a befoglalt ívet is irányíthatjuk az első szögszárral való metszésponttól a második szögszárral való metszéspont felé. Nem zárjuk ki azt sem, hogy az egyik szögszár érintő legyen; ez esetben az ezzel a szárral való ,,második metszéspont'' is jelentse az érintés pontot (5. ábra).
 
 

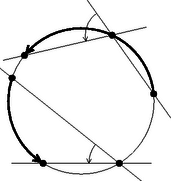5. ábra
 

A kerületi szög ilyen értelmezésével megengedtünk olyan eseteket is, amelyeknél a szög csúcsa a befoglalt köríven van és nem csak a 180∘-ra kiegészítő szöget tekintjük mint a teljes körré kiegészítő íven nyugvó kerületi szöget.*
A következő tételt bizonyítjuk be:
Adott kör két (irányított) kerületi szöge akkor és csak akkor foglal be nagyságra és irányra egyenlő íveket, ha egyenlők.
A tételből nyilvánvalóan következik az előző megjegyzésben kimondott tétel. Ha ugyanis A, B, U, V egy körön fekszik, akkor az AU, AV egyenesek szöge is, a BU, BV egyeneseké is ugyanazt az UV ívet foglalja magába, tehát egyenlők.
Ha viszont AU és AV nagyságra és irányra ugyanakkora szöget határoz meg, mint BU és BV, akkor először is nem lehet A, B és U egy egyenesen, mert akkor AU-val, ill. BU-val egyenlő szöget bezáró egyenesek párhuzamosak lennének, nem lehetne egy közös V metszéspontjuk, kivéve, ha egybeesnek ekkor sincs azonban egy meghatározott V metszéspont.
Létezik tehát egy egyértelműen meghatározott, A-n B-n, és U-n átmenő kör. Messe ez AV-t V'-ben. Ekkor BU és BV' szöge megegyezik AU és AV szögével, tehát feltétel szerint BU és BV szögével is, BV tehát egybeesik BV'-vel és így AV-vel való V metszéspontja is V'-vel. Ez azonban éppen azt jelenti, hogy A, B, U, V egy körön van, és ezt akartuk belátni.
Bizonyítsuk be ezután a fönt kimondott tételt, legyen a körben két kerületi szög. Az egyiket alkossák az e és f egyenesek, a másikat a g és h egyenesek. Forgassuk el az utóbbit úgy, hegy az elforgatott g1 és h1 egyenes közül g1 legyen párhuzamos e-vel. Jelöljük a szögek csúcsát A-val, ill. B-vel, e, f, g1, h1 másik metszéspontját a körrel E, F, G1, H1-gyel (6. ábra).
 
 

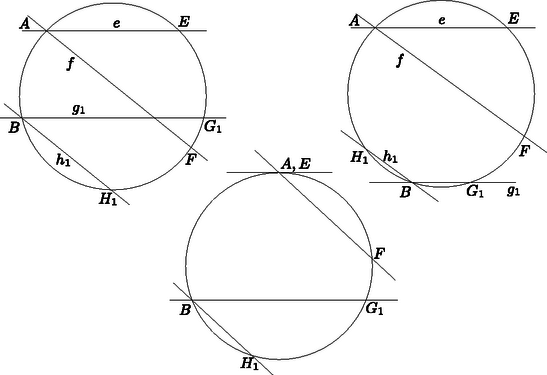6. ábra
 

 
Két állítást kell belátnunk.
a) A szögek egyenlőségéből következik az íveké: ha e és f szöge megegyezik g1 és h1 szögével, akkor h1 is párhuzamos f-fel. Az AE és BG1 párhuzamos húrok felező merőlegese a körnek egyaránt átmérője és párhuzamosak, tehát egybeesnek. Az EG1 ívnek erre az átmérőre vett tükörképe az AB ív, ezek tehát egyenlők és ellentétes irányúak. Hasonlóan az FH1 ív is egyenlő AB-vel és ellentétes irányú, tehát EG1 és FH1 egyező irányú és nagyságú. Ekkor azonban EF és G1H1 is egyező irányú és nagyságú, mert az előbbi az EG1 és G1F ívek összege, az utóbbi pedig G1F-ből az FH1 ív hozzáadásával keletkezik.
b) Az ívek egyenlőségéből következik a szögeké: Ha az EF és G1H1 ívek irányra is, nagyságra is megegyeznek, akkor EG1=EF+FG1 és FH1=FG1+G1H1 ívek is megegyeznek. Mivel e∥g1 most is fennáll, így EG1 és AB egyező nagyságú és ellentétes irányú ívek. Ekkor azonban ugyanez áll az AB és FH1 ívekre is. Ha tehát tükrözünk az AF húrt merőlegesen felező átmérőre, akkor B tükörképe H1 lesz. Eszerint a BH1 egyenes, vagyis h1 is merőleges a tükörtengelyre, tehát párhuzamos f-fel. Ekkor azonban g1 és h1 szöge megegyezik e és f szögével, és ezt kellett belátnunk.
 
II. megoldás. A P pont rombusz esetén a BD átló egyenesének a paralelogrammán kívüli részén van, mert a BD-re való tükrözés A-t C-be és így a BAP szöget a BCP szögbe viszi át.
Ha a paralelogramma nem rombusz, akkor mérjük az A-ból induló és B-n átmenő félegyenesre az AB1=AD távolságot. A B1-en át AD-vel párhuzamosan húzott egyenes messe a CD egyenest C1-ben. Egy P1 pont, amely az AB1C1D paralelogrammára vonatkozóan elégíti ki a feladat feltételeit, a DB1 átló egyenesén van. Szimmetria folytán feltehetjük, hogy a B1-en túli meghosszabbításon (7. ábra).
 
 

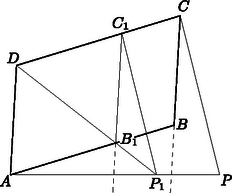7. ábra
 

Toljuk el a B1C1P1, szöget úgy, hogy B1C1 menjen át BC-be. Ekkor P1 az AP1 egyenes mentén mozdul el és jut a P pontba. Ez a BC egyenes ellenkező partján van mint A, másrészt az egész A-ból induló P1-en átmenő félegyenes AB ellenkező partján van, mint a paralelogramma. Így P az AB és CB egyenesek B-n túli meghosszabbításai határolta síkrészben van.
Messe AB és CB egyenese a CP, ill. AP egyenest E-ben, ill. F-ben. Megmutatjuk, hogy az APCD és EPFB négyszögek hasonlóak, a csúcsokat felsorolt sorrend szerint feleltetve meg egymásnak. (8. ábra)
 
 

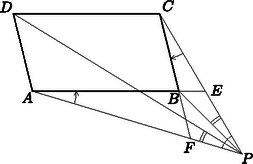8. ábra
 

Valóban P-nél levő szögük közös; másrészt EBF∢=ABC∢, mert egymás csúcsszögei, viszont ABC∢=ADC∢; végül BEP∢=DCP∢=DAP∢. Az utóbbi egyenlőség épp a feladat feltétele folytán áll fenn.
Az ABF és CBE háromszög hasonló, mert A-nál és C-nél feltétel szerint egyenlő szög van, a B-nél levő szögek pedig csúcsszögek. Ebből következik, hogy
BEBF=BCBA=ADCD,
azaz a két négyszög egy-egy egymásnak megfelelő oldalpárjának az aránya is megegyezik. Ebből már következik a két négyszög hasonlósága és ebből az, hogy az átlók az egymásnak megfelelő oldalakkal egyenlő szöget zárnak be. Így APD∢=EPB∢=CPB∢. Ezzel a feladat állítását bebizonyítottuk.
*Az ábrán a szögek iránya ellentétes

*Ezért látszott célszerűbbnek befoglalt ívről beszélni, mint arról az ívről, amin a szög nyugszik.