Feladat: 1975. évi Kürschák matematikaverseny 2. feladata Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Miklós Dezső ,  Moussong Gábor 
Füzet: 1976/február, 55 - 57. oldal  PDF  |  MathML 
Témakör(ök): Egyéb sokszögek geometriája, Négyszögek geometriája, Rombuszok, Egyenlő szárú háromszögek geometriája, Geometriai egyenlőtlenségek, Beírt alakzatok, Háromszögek hasonlósága, Vetítések, Trapézok, Súlyvonal, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1976/február: 1975. évi Kürschák matematikaverseny 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. A feladatban megfogalmazott állítás nem igaz. Ennek belátására elég megadni egy sokszöget, amelybe írható négyszög úgy, hogy minden oldala nagyobb, mint bármelyik beírt rombusz oldala.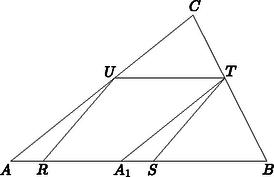
Sokszögnek olyan egyenlőszárú háromszöget választunk, amelyiknek a szárai kisebbek a harmadik oldalnál. Megmutatjuk először, hogy minden ebbe beírható rombusz oldala kisebb egy, a legnagyobb oldal felénél kisebb d távolságnál.
Általában, egy háromszögbe beírt négyszöghöz van a háromszögnek olyan oldala, amelyikre két négyszögcsúcs esik. Essék az ABC háromszögbe írt RSTU rombusz R, S csúcsa az AB oldalra, legyen URS∢≤90∘ és válasszuk a háromszög betűzését úgy, hogy R közelebb legyen A-hoz, mint S, egybe is eshet vele. Húzzunk T-ből párhuzamost AC-vel, messe ez AB-t A1-ben (1. ábra).

 
 

1. ábra
 

Ekkor az A1BT háromszög hasonló az ABC háromszöghöz, és AA1=UT=RS, így
AB=RS+A1B=RS+A1BST⋅ST.
Mivel a jelölést úgy választottuk, hogy URS∢≤90∘, így A1ST∢=180∘-TSB∢=180∘-URS∢≥90∘, tehát ST<A1T, kivéve ha R és A, s így egyben S és A1 is egybeesik. Továbbá ST=RS. Ezeket felhasználva
AB≥RS(1+A1BA1T)=RS(1+ABAC),
azaz
RS≤AB1+ABAC=11AB+1AC.
Ez akkor a legnagyobb, ha AB és AC a háromszög két legnagyobb oldala, és akkor is kisebb a legnagyobb oldal felénél, kivéve, ha AB=AC≥BC.
Ezzel fenti állításunkat igazoltuk: ha AB>AC=BC, akkor semelyik beírt rombusz oldala sem nagyobb, mint
d=11AB+1AC,  ami kisebb, mint  12AB.

Azt kell még megmutatnunk, hogy írható az ABC háromszögbe olyan négyszög, amelyiknek mindegyik oldala nagyobb d-nél. Válasszuk a négyszög csúcsainak az AB oldal F felezőpontját, A-t, C-t, továbbá a BC oldalnak egy olyan E pontját, amelyiknek a merőleges vetülete AB-n d-nél nagyobb távolságra esik F-től (2. ábra). Ekkor a négyszög minden oldalának a merőleges vetülete AB-n nagyobb d-nél, tehát az oldalak is nagyobbak. Ezzel a feladatban megfogalmazott állítást megcáfoltuk.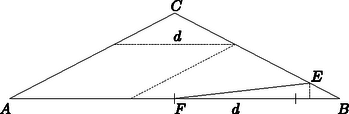
 
 

2. ábra
 

Megjegyzések. 1. A fenti meggondolás azt is mutatja, hogy a rombusz oldalára talált felső korlát elérhető, ha a rombusz csúcsa egybeesik a két legnagyobb oldal közös csúcsával.
2. Többen felvetették a kérdést, vajon írható-e minden konvex sokszögbe rombusz. A feladat szempontjából nem lényeges ez a kérdés, hiszen a megfogalmazott állítást cáfoltuk. Ha a most feltett kérdésre tagadó lenne a válasz, az mindössze egy más természetű ellenpéldára vezetne.
Nem nehéz azonban látni, hogy ez az eset nem léphet fel, sőt tetszés szerinti irányhoz beírható olyan rombusz, amelynek egyik átlója ezzel az iránnyal párhuzamos. Valóban, a sokszög adott iránnyal párhuzamosan húzható szelőinek a felezőpontjai egy törtvonalon helyezkednek el. Húzzunk ugyanis minden csúcson át az iránnyal párhuzamos szelőt. Ezek trapézokra és általában két vagy egy, esetleg 0 háromszögre bontják a sokszöget. A háromszögbeli szelők felezőpontjai egy súlyvonalon, a trapézbeliekéi a párhuzamos oldalak felezőpontjait összekötő szakaszon helyezkednek el.
Az eljárást megismételve az adott irányra merőleges iránnyal is, a keletkezett két törtvonal közös pontja olyan lesz, hogy azon át az adott iránnyal párhuzamost és arra merőlegest húzva ezek egy rombusz csúcsait metszik ki a sokszög határából (3. ábra).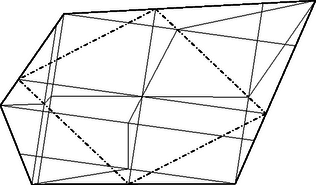
 
 

3. ábra
 

Egy versenyző más meggondolással azt is megmutatta, hogy tetszés szerinti irányt adva meg, olyan beírt rombusz is létezik, amelyiknek az egyik oldalpárja adott irányú.