Feladat: 1973. évi Kürschák matematikaverseny 3. feladata Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Bacsó Gábor ,  Kertész Gábor ,  Kollár János 
Füzet: 1974/február, 54 - 55. oldal  PDF  |  MathML 
Témakör(ök): Térgeometria alapjai, Térelemek és részeik, Kombinatorikus geometria térben, Tetraéderek, Kombinatorikai leszámolási problémák, Háromszögek nevezetes tételei, Egyéb sokszögek geometriája, Kör geometriája, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1974/január: 1973. évi Kürschák matematikaverseny 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Nevezzük röviden csúcspontnak az olyan pontot, mely három adott sík közös pontja. A feltételek szerint bármely három sík egyetlen csúcspontot határoz meg.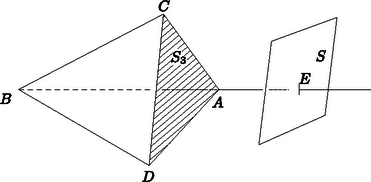
Jegyezzük meg továbbá, hogy négy adott sík mindig közrezár egy (és csakis egy) tetraédert. Ennek belátását az olvasóra bízzuk. Természetesen e tetraéderbe más sík belemetszhet, tehát általában nem szerepel a tekintett térrészek között.
Legyen mármost S egy adott sík és P olyan csúcspont, mely nincs az S síkon, de az összes olyan csúcspont között, mely S-nek P-vel azonos oldalán helyezkedik el, S-hez legközelebb van. Legyenek S1, S2, S3 a P-t meghatározó síkok. Ekkor S, S1, S2, S3 egy T tetraédert zár közre. Állítjuk, hogy a T tetraédert további adott sík nem metszi, tehát T egyike azon térrészeknek, melyekre az n sík a teret darabolja.
Tegyük fel, hogy egy további adott S' sík metszi a T tetraédert. Legyenek A, B, C a tetraéder P-től különböző csúcsai; A, B, C az S síkon helyezkedik el. Nyilvánvalóan kell, hogy az S' sík messe az AP, BP, CP szakaszok valamelyikét. Tegyük fel például, hogy S' az AP szakaszt metszi egy Q pontban. Ekkor Q is csúcspont, hiszen AP két adott sík metszésvonala, és így Q három adott sík metszéspontja. De Q közelebb van S-hez, mint P, ami ellentmond P választásának.
A fentiek alapján az adott síkok bármelyikéhez találhatunk rá támaszkodó tetraédert a síkok által létrehozott térrészek között. Sőt, ha S olyan sík, melynek mindkét oldalán van csúcspont, akkor S-re két ilyen tetraéder is támaszkodik.
Állítjuk, hogy legfeljebb három síknak lehet minden csúcspont ugyanazon az oldalán. Tegyük fel, hogy négy ilyen sík is volna, S1, S2, S3, S4. Legyen ABCD az S1, S2, S3, S4 által alkotott tetraéder, ahol S1 az ABC, S2 az ABD, S3 az ACD, S4 a BCD síkkal azonos. Mivel n≥5, van egy további S sík az adott síkok között. Az S sík nyilván nem metszheti az ABCD tetraéder valamennyi élét, tehát például az AB él egyenesét egy, az élhez nem tartozó E pontban metszi. Legyen például E az AB egyenes A-ból kiinduló, B-t nem tartalmazó félegyenesén. Mármost E és B az S3=ACD sík különböző oldalain elhelyezkedő csúcspontok, ami ellentmondás (1. ábra).

 
 

1. ábra
 

Számoljuk mármost össze a síkok által létrehozott térrészek közti tetraédereket úgy, hogy minden síkhoz megszámoljuk a rá támaszkodókat. Láttuk az előbb, hogy legfeljebb három kivételével minden síkra legalább két tetraéder támaszkodik; a ,,kivételes'' síkokra legalább egy. Így legalább 2n-3 tetraédert számolunk. Mivel azonban minden tetraédert négyszer számolhattunk (a négy lapsíkjánál), a tetraéderek száma legalább 2n-34, amit bizonyítani akartunk.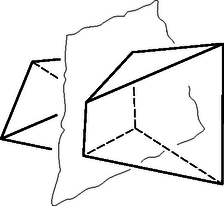
 
Megjegyzések: 1. Több versenyző ,,felhasználta'', hogy ha egy tetraédert síkkal metszünk, akkor keletkező darabjainak egyike tetraéder. Ez az állítás nem igaz; ha egy tetraédert olyan síkkal metszünk, mely két kitérő élét elválasztja (de egyiket sem metszi), akkor két ,,háztető'' (ötlapú test) keletkezik (2. ábra).
 
 

2. ábra
 

2. A feladat egyszerűbb változata síkbeli probléma: ha n egyenes a síkban úgy helyezkedik el, hogy semelyik kettő nem párhuzamos és semelyik három nem halad át egy ponton, akkor az általuk létrehozott síkrészek között legalább 2n-23 háromszög van. Ez az állítás a térbeli feladathoz hasonlóan igazolható.
3. Felvetődik a kérdés, hogy a 2n-34 korlát mennyire éles, vagyis nem bizonyítható-e ennél erősebb állítás. Hasonló kérdezhető a 2. pontban említett feladattal kapcsolatban is. Erre a problémára külön cikkben visszatérünk.