| Feladat: | 1970. évi Kürschák matematikaverseny 3. feladata | Korcsoport: 18- | Nehézségi fok: nehéz |
| Megoldó(k): | Bajmóczy Ervin , Füredi Zoltán , Kóczy László , Martoni Viktor , Ruzsa Imre | ||
| Füzet: | 1971/május, 197 - 198. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Egyéb szinezési problémák, Természetes számok, Oszthatóság, Kombinatorikai leszámolási problémák, Háromszögek nevezetes tételei, Teljes indukció módszere, Kürschák József (korábban Eötvös Loránd) | ||
| Hivatkozás(ok): | Feladatok: 1971/február: 1970. évi Kürschák matematikaverseny 3. feladata | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. Megoldás. Megadunk egy utasítást arra, hogyan kell a még nem színezett szakaszokat színezni. Legyen egy olyan szakasz, amelynek végpontjai az adott pontok közül valók és amely még nincs kiszínezve. A feltétel szerint létezik egy és csakis egy olyan törött vonal, mely eredetileg színezett szakaszokból áll és -t -vel köti össze. Jelölje ezt a törött vonalat. Legyen mármost az szakasz piros, ha páros sok kék szakaszt tartalmaz. (Megjegyezzük, hogy ez a ,,színezési szabály'' akkor is érvényes, ha már eleve is színezett volt.) Megmutatjuk, hogy a fenti ,,színezési szabály'' kielégíti a feladat követelményeit. Legyen e célból tetszőleges háromszög, melynek csúcsai az adott pontok közül valók. Először is megadható olyan pont, melyből az -ba, -be, -be vezető, eredetileg színezett szakaszokból álló , , utaknak nincsen -től különböző közös pontjuk (megengedjük itt, hogy egybeessen pl. -val, ekkor egyetlen pontból áll). Tekintsük ugyanis az -t -vel összekötő, eredetileg színezett szakaszokból álló utat. -ből felé elindulva a úton, előbb-utóbb elérjük a út valamely pontját (ha rajta fekszik a úton, akkor ; természetesen az is előfordulhat, hogy vagy ). Könnyen látható, hogy az így megszerkesztett pont a fenti kikötésnek eleget tesz (5. ábra). 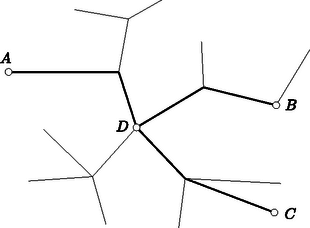 5. ábra Mármost a fenti színezési szabály szerint, az , , szakaszok között rendre annyi kék van, ahány páratlan szám előfordul az és utakon fekvő kék szakaszok száma és és utakon fekvő kék szakaszok száma között. Mivel páros (hiszen , , utak minden kék szakasza kétszer van beszámítva ebbe az összegbe), az háromszögnek valóban páros sok kék oldala van. Ezek után a következő ,,színezési szabályt'' adhatjuk meg: az él legyen kék, ha , különböző színűek. Tekintsünk mármost egy tetszőleges háromszöget, melynek csúcsai az adott pontok közül valók. Ha , , azonos színűek, akkor az , , szakaszok mindegyike piros. Ha, mondjuk és azonos és tőlük különböző színű, akkor piros, és kék. A piros szakaszok száma tehát vagy 3 vagy 1, mindenképpen páratlan. Tehát a megadott ,,színezési szabály'' a feladat kikötésének eleget tesz. 2. Megmutatható ‐ erre több versenyző utalt is ‐, hogy a szakaszoknak a feladatbeli színezése egyértelmű. Legyen ugyanis tetszőleges szakasz. A feltétel szerint és összeköthető egy, eleve színezett élekből álló 3. Elegendő volna a feladatban annyit feltenni, hogy bármely két pont legfeljebb egyféleképpen köthető össze eredetileg is megszínezett szakaszokból álló törött vonallal. Ilyenkor ugyanis (mint az könnyen igazolható) meg lehet még néhány további szakaszt színezni úgy, hogy a kapott szakaszokra már a feladat feltétele teljesüljön. |