Kezdőlap


Feladat:	1968. évi Kürschák matematikaverseny 2. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bajmóczy Ervin , Lempert László , Michaletzky György , Ruzsa Imre , Soltész János , Somorjai Gábor , Takács László
Füzet:	1969/november, 98 - 99. oldal		PDF \| MathML
Témakör(ök):	Kör geometriája, Vetítések, Derékszögű háromszögek geometriája, Háromszög-egyenlőtlenség alkalmazásai, Skatulyaelv, Egyenlőtlenségek, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):	Feladatok: 1969/január: 1968. évi Kürschák matematikaverseny 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

textbfMásodik feladat. Adott a síkban egy egyenes, egy $n$

Megoldás. Vetítsük a

4 n

szakasz mindegyikét az adott egyenesre (ezt vízszintesnek mondjuk) és egy rá merőleges (függőlegesnek mondott) egyenesre. A vízszintes vetületek hossza legyen

a_{1}

a_{2}, ..., a_{4 n}

, a függőlegeseké pedig

b_{1}

b_{2}, ..., b_{4 n}

. A feladat állítása egyértelmű azzal a kijelentéssel, hogy vagy a vízszintes, vagy a függőleges vetületek között van kettő, amelyeknek van közös pontjuk.
Az

i

-edik szakasz olyan (esetleg szakasszá elfajuló) derékszögű háromszög átfogója, amelynek vízszintes befogója

a_{i}

, függőleges befogója pedig

b_{i}

hosszúságú (1. ábra).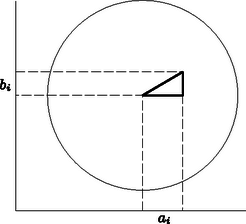

1. ábra

Minthogy a háromszög két oldalának összege a harmadiknál nagyobb,

\begin{matrix} a_{i} + b_{i} \geq 1. \end{matrix}

Itt az egyenlőséget is meg kellett engednünk, mert számolunk azzal, hogy a vetített szakasz vízszintes vagy függőleges. Eredményünkből következik, hogy mind a

4 n

szakasz vetületeinek összege

\begin{matrix} \sum a_{i} + \sum b_{i} \geq 4 n . \end{matrix}

Itt és a következőkben is minden összegezés az

i = 1,2, ...,4 n

értékekre terjed ki.
Ha a vízszintes vetületek között nincs két közös pontú, akkor ezek együttesen nem fedik le az

n

-sugarú kör

2 n

hosszúságú vízszintes vetületét, tehát

\begin{matrix} \sum a_{i} < 2 n . \end{matrix}

Ugyanígy, ha a függőleges vetületek között nincs két közös pontú, akkor

\begin{matrix} \sum b_{i} < 2 n . \end{matrix}

Ha tehát egyik eset sem következik be, akkor

\begin{matrix} \sum a_{i} + \sum b_{i} < 4 n . \end{matrix}

Ez ellentmond fenti eredményünknek. Kell tehát, hogy a mondott két eset valamelyike bekövetkezzék, ami ‐ mint megállapítottuk ‐ a feladat állításának helyességét mondja ki.

Megjegyzés. A feladat megoldásakor zárt szakaszokra gondoltunk, azaz a szakaszokhoz végpontjaikat is hozzászámítottuk. Igaz azonban a feladat állítása nyílt, tehát végpontjaiktól megfosztott szakaszokra is, ennek bizonyításához azonban ki kell egészítenünk megoldásunkat.
Ha nyílt szakaszokkal dolgozunk, akkor a kör

2 n

hosszúságú vetületén elhelyezkedő, közös pont nélküli vetületi szakaszok hosszának összege

2 n

is lehet, hiszen most a végpontjukkal érintkező szakaszoknak nincs közös pontja. Így tehát csak

\sum a_{i} \leq 2 n

\sum b_{i} \leq 2 n

és ezekből a

\begin{matrix} \sum a_{i} + \sum b_{i} \leq 4 n \end{matrix}

eredményhez juthatunk, ami nem jelent ellentmondást.
Ha azonban így nem jutunk ellentmondáshoz, tehát a feladat állításának bizonyításához sem, akkor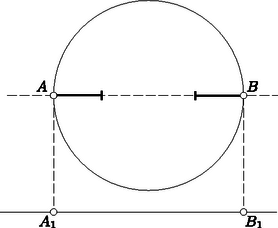

\begin{matrix} \sum a_{i} + \sum b_{i} = 4 n, \end{matrix}

tehát

\sum a_{i} = 2 n

. Ez azt jelenti, hogy a vízszintes vetületek (végpontjaikkal együtt) a kör teljes vízszintes vetületét, az

A_{1} B_{1}

szakaszt beborítják (2. ábra).

2. ábra

Ekkor a vetületek között van

A_{1}

kezdőpontú és

B_{1}

végpontú is. Ilyen vetületet azonban csak a kör vízszintes

A B

átmérőjén elhelyezkedő szakaszok adhatnak. Ebben az eddig el nem intézett esetben tehát az adott egyenessel párhuzamos

A B

egyenes kielégíti a feladat követelményét, hiszen nemcsak közös pontja van két szakasszal, hanem tartalmazza is azokat.