Feladat: 1967. évi Kürschák matematikaverseny 3. feladata Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Grosz Tamás ,  Kóczy László ,  Mérő László 
Füzet: 1968/május, 197 - 202. oldal  PDF  |  MathML 
Témakör(ök): Négyszögek geometriája, Paralelogrammák, Háromszögek nevezetes tételei, Háromszögek hasonlósága, Egyéb sokszögek hasonlósága, Vetítések, Trigonometriai azonosságok, Eltolás, Egyenlő szárú háromszögek geometriája, Derékszögű háromszögek geometriája, Háromszögek egybevágósága, Vektorok lineáris kombinációi, Vektorok felbontása összetevőkre, Vektorok skaláris szorzata, Trigonometrikus függvények, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1968/február: 1967. évi Kürschák matematikaverseny 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Segédtételként fel fogjuk használni, hogy egy konvex szögtartomány két pontjának a száregyenesektől való távolságait összeadva akkor és csak akkor kapunk ugyanakkora összeget, ha a két pont összekötő egyenese a szögfelezőre merőleges.
Tekintsük ennek bizonyítása végett az AOB konvex szögtartományban elhelyezkedő P pontot. Messe a P pontból a szögfelezőre bocsátott merőleges a szárakat az A, B pontokban (5. ábra).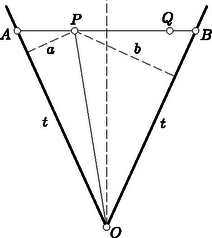

 
 

5. ábra
 

Legyen OA=OB=t és a P pontnak az OA, OB egyenesektől való távolsága a és b. Minthogy az AOBΔ területe az AOPΔ és BOPΔ területének összege, e terület kétszerese at+bt=(a+b)t. Eszerint a
(P,AOB∢)=a+b
távolságösszeg az AB szakasz minden pontjára ugyanakkora, és akkora, mint az A pont távolsága az OB egyenestől. Minthogy azonban az OA szár minden pontja az OB egyenestől más-más távolságra van, a P és Q pontok akkor és csak akkor adnak ugyanakkora távolságösszeget, ha belőlük a szögfelezőre merőlegest bocsátva az OA szárnak ugyanahhoz a pontjához jutunk, ha tehát a PQ egyenes a szögfelezőre merőleges.
A bizonyításra térve feltesszük, hogy a feladat követelménye a konvex ABCD négyszögre teljesül. A bizonyítást kisérő 6. ábra szándékosan torz, hiszen éppen azt kell bizonyítanunk, hogy csak paralelogramma adhatja a helyes ábrát, és ilyen ábra annak felhasználására csábítana, amit bizonyítani akarunk.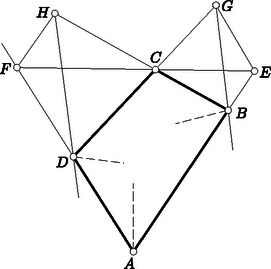
 
 

6. ábra
 

A C ponton át a BAD∢ felezőjére merőlegest bocsátunk. Messe ez az AB, AD szárakat az E, F pontokban. Az E ponton át AD-vel párhuzamost húzunk, s ez a DC egyenest G-ben metszi. Hasonlóan legyen H a BC egyenes és az F-en át AB-vel húzott párhuzamos metszéspontja. A CBEΔ és CHFΔ, valamint ugyanígy a CGEΔ és CDFΔ hasonló, mert oldalaik páronként egy egyenesen vannak, illetőleg párhuzamosak. Ebből következik, hogy a CBEG és CHFD négyszögek is hasonlók, hogy ezért CBG∢=CHD∢, hogy tehát a BG és DH egyenesek párhuzamosak.
Segédtételünk szerint (C,DAB∢)=(E,DAB∢), a párhuzamosság miatt (E,DAB∢)=(G,ADC∢), a feladat feltevése szerint pedig (C,DAB∢)=(B,ADC∢). Ezekből (G,ADC∢)=(B,ADC∢) következik, tehát segédtételünk szerint az is, hogy a GB egyenes az ADC∢ felezőjére merőleges. Ugyanígy következik, hogy HD merőleges az ABC∢ felezőjére. Minthogy azonban a most említett egyenesek párhuzamosak, az ABC∢ és ADC∢ felezői is párhuzamosak. Ha tehát a DCB∢-et egy ezekkel a szögfelezőkkel párhuzamos egyenesre tükrözzük, szárai a DAB∢ száraival párhuzamos helyzetbe jutnak. Ezért e szögek egyenlők, azaz az ABCD négyszögben A-nál és C-nél egyenlő szögek vannak. Ugyanígy adódik, hogy a négyszög másik két szemközti szöge is egyenlő, tehát a négyszög paralelogramma.
A paralelogrammának valóban megvan a feladatban leírt tulajdonsága, mert bármely csúcsból indulunk is ki, mindig a két magasság összegéhez jutunk. (Ez a megoldás Pogáts Ferenctől és Herczeg Jánostól való.)
 
II. megoldás. Felhasználjuk azt, hogy ha egy konvex φ szög egyik szárára a csúcstól felmérjük a t távolságot, a végpont a másik szár egyenesétől tsinφ távolságra van.
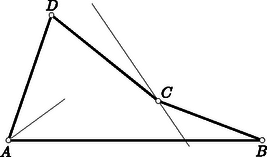
A négyszög betűzését úgy választjuk meg, hogy az AB és DC félegyenesek és ugyanígy a CB és DA félegyenesek messék egymást vagy párhuzamosak legyenek (7. ábra).
 

 

7. ábra
 

Legyen β és α e félegyenespárok hajlásszöge, párhuzamosság esetén tehát α=0 és β=0 is lehetséges. Legyen továbbá ABC∢=π-φ s így BCD∢=β+φ.
Jelölje C1 és C2 a C pont vetületét az AD, AB egyeneseken, B1, B2 és B3 pedig a B pont vetületét az AD, CD és CC1 egyeneseken. Ha a feladat követelménye a B és C csúcsokra teljesül, akkor
CC1+CC2=BB1+BB2.
Minthogy CC1-BB1=CB3,
CB3+CC2=BB2,
amit e megoldás első bekezdése alapján
BCsinα+BCsin(π-φ)=BCsin(β+φ)
alakban írhatunk, hiszen az itt fellépő távolságokhoz úgy jutunk, hogy a CBB3∢=α,ABC∢=π-φ és BCD∢=β+φ szög egyik szárára felmérjük a BC szakaszt, s a kapott végpontnak a másik szár egyenesétől való távolságát tekintjük.
Utolsó egyenletünkből BC-vel osztva
sinα+sinφ=sinβcosφ+cosβsinφ
adódik. Ehhez hasonlóan, a feladat követelményének az A, B csúcsokra való teljesülésére építve azt kapjuk, hogy
sinβ+sinφ=sinαcosφ+cosαsinφ.
Utolsó két egyenletünket összeadva
(sinα+sinβ)(1-cosφ)+(2-cosα-cosβ)sinφ=0.
Itt 0<φ<π miatt mindkét tag második tényezője pozitív, első tényezőik viszont nem-negatívak. Az egyenlőség tehát csak úgy állhat fenn, ha
sinα+sinβ=0,cosα+cosβ=2.
Mivel 0≤α<π és 0≤β<π, mindkét eredményünkből α=β=0 következik, ami éppen azt jelenti, hogy az ABCD négyszög parallelogramma.
 
Megjegyzés. Ez a megoldás valamivel egyszerűbbé válik, ha a jelölést úgy választjuk meg, hogy sinα≥sinβ is teljesüljön. Ekkor elég az előző bekezdés alsó egyenletére építenünk, mert ez
(sinα-sinβ)+sinβ(1-cosφ)+(1-cosβ)sinφ=0
alakban írható. Itt egyik tag sem lehet negatív, és összegük 1-cosφ és sinφ pozitivitása miatt csak akkor lehet 0, ha
sinα=sinβ,sinβ=0,cosβ=1,
amiből α=β=0 következik.
 
III. megoldás. Abból a megállapításból indulunk ki, hogy ha egy négyszög eleget tesz a feladat követelményének, akkor az olyan másik négyszög is eleget tesz, amelynek oldalai az első négyszög oldalaival rendre párhuzamosak. Ez közvetlenül kiolvasható abból, hogy második megoldásunk a követelmény teljesülését szögek közötti összefüggésekkel fejezte ki. Nem kell azonban ehhez szögfüggvényekre sem hivatkoznunk. Elegendő annak megállapítása, hogy a 7. ábra szaggatott vonallal körülkerített részét a BC szakasz és a négy oldalirány már meghatározza. Ha tehát egy rendre párhuzamos oldalakkal bíró másik négyszögből indulunk ki, az előbbihez hasonló ábrarészhez jutunk. Eszerint a feladat követelményének a B, C pontokra való teljesülését biztosító CB3+CC2=BB2 összefüggés megfelelője a másik négyszögre is teljesül. Ezért ez a négyszög is kielégíti a feladat követelményét, hiszen a B, C csúcsok szerepét itt bármely két csúcs átveheti.
A feladat követélményét kielégítő négyszög egyik oldalegyenesét párhuzamosan eltolva elérhetjük, hogy az új konvex ABCD négyszög két szomszédos oldala egyenlő legyen, pl. AB=CB (8. ábra).
 
 

8. ábra
 

Jelölje A1, A2 és C1, C2 az A és C pont vetületét a CB, CD és AB, AD egyeneseken. Minthogy fenti megállapításunk szerint a feladat követelménye az új négyszögre is teljesül,
AA1+AA2=CC1+CC2,
tehát az ABCΔ egyenlő szárúságából következő AA1=CC1 miatt
AA2=CC2.
Ezért a derékszögű ACA2Δ és CAC2Δ egybevágó, s így ACA2∢=CAC2∢. Az ABCΔ alapján nyugvó szögek egyenlőségét is figyelembe véve azt kapjuk, hogy az új négyszögben A-nál és C-nél elhelyezkedő szögek egyenlők, s ezért ez az eredeti négyszög megfelelő szögeire is áll. Ugyanígy adódik a másik két szemközti szög egyenlősége, tehát az is, hogy paralelogrammáról van szó. (Ez a megoldás Böröczki Károlytól való.)
 
IV. megoldás. A feladat mit sem változik, ha benne nem a csúcsnak a rajta át nem haladó oldalegyenesektől való távolságait adjuk össze, hanem mind a négy oldalegyenestől való távolság összegéről szólunk, hiszen a csúcson áthaladó oldalegyenestől való távolság 0. A feladatot most ebben az alakban tekintjük, és megoldásához a vektorokra vonatkozó alapismereteket is felhasználunk.
Legyen n egy félsík határegyenesére merőleges, a félsík belseje felé mutató egységvektor. Legyen A és B a félsík két pontja, a és b pedig e pontok távolsága a határegyenestől (9. ábra).
 

9. ábra
 

Felhasználjuk, hogy e távolságok különbsége, azaz az A-ból B-be vezető v vektor n-nel párhuzamos összetevőjének előjeles hossza
b-a=vn.
Legyenek n1, n2, n3, n4 a feladat követelményeit kielégítő négyszög oldalaira merőleges, a négyszög belseje felé mutató egységvektorok, továbbá a és b a négyszög két egymáshoz csatlakozó oldalvektora (10. ábra).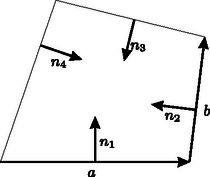
 

10. ábra
 

Minthogy a két végpontjára a négy oldalegyenestől való távolság összege ugyanakkora, e két összeg különbsége, azaz a megfelelő távolságok különbségeinek összege 0. A fentiek szerint tehát
an1+an2+an3+an4=a (n1+n2+n3+n4)=0.
A b vektorra ugyanígy
b (n1+n2+n3+n4)=0
adódik. Eszerint n1+n2+n3+n4 merőleges az egymással nem párhuzamos a, b vektorok mindegyikére, ami csak úgy lehetséges, ha
n1+n2+n3+n4=0.
Ha tehát e négy vektort egymáshoz fűzzük, zárt négyszöget kapunk. E négyszög mindegyik oldala egységnyi, tehát rombusz és szemközti oldalai párhuzamosak. Ezért az eredeti négyszög rájuk merőleges szemközti oldalai is párhuzamosak, és e négyszög valóban paralelogramma.
 
Megjegyzések. 1. A feladat konvex négyszögről szólt. Megmutatjuk, hogy ez a megszorítás felesleges, mert konkáv négyszögre a feladat követelménye nem teljesülhet. Legyen az ABCD négyszögben a C csúcsnál konkáv szög. A C csúcson át a DAB∢ felezőjére merőlegest állítunk. Ez a négyszögnek legalább egy csúcsát, pl. a B csúcsot elválasztja az A csúcstól (11. ábra), hiszen a konkáv szög nem helyezkedhetik el a merőleges egyenesnek egy oldalán.
 

 

11. ábra
 

Ezért az első megoldás segédtétele szerint az ott használt jelöléssel (C,DAB∢)<(B,DAB∢). Minthogy itt a jobboldalon a B pontnak az AD egyenestől való távolsága áll, s ez kisebb, mint a B pontnak az AD, CD egyenesektől való távolságainak összege, a feladat követelménye a B és C csúcsokra valóban nem teljesülhet.
A feladat követelése konkáv négyszögekre akkor sem teljesülhet, ha az oldalegyenesektől való távolságokat előjellel látjuk el, negatívnak mondva a távolságot, ha a pont az oldalegyenesnek a másik oldalán van, mint amerről a négyszög az oldalra támaszkodik. Negyedik megoldásunk ezt is bebizonyítja.
2. A második és negyedik megoldás mutatja, hagy a feladat állításának helyességét már az is biztosítja, ha csak három csúcsra követeljük meg a távolságösszegek egyenlőségét. Ha ez az összeg három csúcsra egyenlő, akkor eszerint a negyedik csúcsra is ugyanakkora.
A legutóbbi mondat megállapítása messzemenően általánosítható. Negyedik megoldásunk mintájára könnyen belátható, hogy ha a síkban véges sok egyenest adunk meg, mindegyiknél megszabva, hogy melyik oldalán elhelyezkedő pontokra mondjuk a pontnak az egyenestől való távolságát pozitívnak és melyikre negatívnak, ha továbbá a sík három nem egy egyenesen levő pontjára az egyenesektől való távolságok összege ugyanakkora, akkor a sík minden pontja ugyanekkora távolságösszeget ad. Ez többek között azt is jelenti, hogy ha egy konvex n-szög esetében három csúcsra az oldalegyenesektől való távolságok összege ugyanakkora, akkor ugyanekkora minden csúcsra, sőt az n-szög minden pontjára is. A negyedik megoldás alapján könnyen belátható, hogy egy konvex n-szögnek akkor van meg a most említett tulajdonsága, ha oldalai egy egységoldalú konvex n-szög oldalaira rendre merőlegesek.