Feladat: 1967. évi Kürschák matematikaverseny 2. feladata Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Babai László ,  Kóczy László ,  Mérő László ,  Surányi László ,  Szeredi Péter 
Füzet: 1968/május, 194 - 197. oldal  PDF  |  MathML 
Témakör(ök): Egyéb sokszögek geometriája, Háromszögek nevezetes tételei, Oszthatóság, Kombinatorikai leszámolási problémák, Ponthalmazok, Részhalmazok, Halmazok számossága, Egyenlőtlenségek, Teljes indukció módszere, Egyéb szinezési problémák, Topológia, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1968/február: 1967. évi Kürschák matematikaverseny 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladatban konvex sokszög szerepel, de ez a megszorítás nyilván lényegtelen, a következőkben nem is támaszkodunk rá. Ilyen megszorítás nélkül azonban zavarhatná a megoldót az a kérdés, vajon felbontható-e minden sokszög egymást nem metsző átlókkal háromszögekre. Ez így van, de ennek bizonyítása nem könnyű.
Lényegtelenül módosul a feladat, ha egymást nem metsző átlókkal való felbontás helyett az n-szöget olyan háromszöghalmaz egyesítéseként állítjuk elő, amelyben minden háromszög minden csúcsa az n-szög csúcsai közül való, s amelyben nincs két egymásra boruló háromszög. Ez az átszövegezés csak annyit változtat, hogy így a feladat az n=3 esetben sem veszti értelmét, mert a háromszöghalmaz egyetlen elemből, magából a háromszögből is állhat. Eszerint ebben az esetben a feladat követelése és állítása is teljesül.

 
I. megoldás. Minden a felbontásban szereplő átló a sokszöget két sokszögre vágja fel. Tekintsük az így keletkező részsokszögek oldalszámának minimumát. Azt állítjuk, hogy ez a minimum 3, hogy tehát szerepel olyan átló, amely sokszögünkből háromszöget vág le. Ha ugyanis a minimum k>3 volna és pl. az A1Ak átló által levágott A1A2...Ak-1Ak sokszög valósítaná meg, akkor kellene, hogy e k-szög egy AiAj átlója is szerepeljen a felbontásban, hiszen háromszögekre való felbontásról van szó. Mivel az AiAj átló által levágott AiAi+1...Aj sokszög oldalszáma k-nál kisebb, k valóban nem lehet minimum.
A vizsgált részsokszögek között van 3-nál nagyobb oldalszámú is, mert különben egy átló a sokszöget két háromszögre bontaná fel, s ennek végpontjaiban a feladat követelésével ellentétben 2 háromszög találkoznék.
A vizsgált részsokszögek között nincs négyszög, mert ezt egy a felbontásban szereplő átlónak két háromszögre kellene felbontania, és így ennek az átlónak egyik végpontjában 2 háromszög találkoznék.
Ezek szerint a vizsgált részsokszögek oldalszámai között van 3-nál nagyobb, s ezek között a 3-nál nagyobb oldalszámok közül a legkisebbnek az értéke legalább 5. Legyen pl. az A1Ak átló által levágott A1A2...Ak-1Ak ilyen legkisebb oldalszámú, de háromszögtől különböző részsokszög. Beláttuk már, hogy 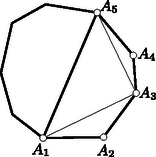k≥5.
 
 

1. ábra
 

Minthogy a felbontás a most említett részsokszöget is háromszögekre bontja fel, felbontásában egy A1AiAk, háromszög is fellép. k minimum-tulajdonsága miatt sem A1Ai, sem AiAk nem vághat le 3-nál nagyobb oldalszámú (és természetesen k-nál kisebb oldalszámú) sokszöget, ezért i≤3 és k-i+1≤3. Ezek az egyenlőtlenségek a fenti k≥5 eredménnyel együtt
0≤k-5≤i-3≤0
alakban írhatók, s innen k=5 és i=3 adódik.
Ezzel beláttuk, hogy sokszögünk felbontásában fellép olyan átló, amely ötszöget vág le, s hogy ezt az ötszöget a felbontó átlók három olyan háromszögre vágják fel, amelyek közül az ötszöget levágó átló végpontjaiban kettő-kettő találkozik (1. ábra). Hagyjuk el eredeti sokszögünkből ezt az ötszöget. Ezáltal a sokszög oldalszáma 3-mal csökken, a megmaradó sokszög átlókkal való felbontása viszont változatlanul eleget tesz a feladat követelményének, hiszen az egy csúcsba futó háromszögek száma csak két csúcsnál ad új értéket, s ott 2-vel csökkent.
Eszerint eljárásunkat a kapott sokszögre újból alkalmazhatjuk, ezt folytatva a sokszög oldalszámát minden lépésben 3-mal csökkenthetjük mindaddig, amíg a maradó sokszögben még van átló, amíg tehát háromszöghöz nem jutunk. Ezért az eredeti sokszög oldalszáma valóban osztható 3-mal.
Megoldásunkból az is kiolvasható, hogy ha n osztható 3-mal, akkor a konvex n-szög felbontható a feladat követelményét kielégítő módon.
 
II. megoldás. A bizonyítást n-re vonatkozó teljes indukcióval végezzük el. A feladat szövege után említettek szerint az állítás az n=3 esetben helyes. Elegendő tehát azt bizonyítanunk, hogy ha a feladat állítása egy n>3 értéknél kisebb oldalszámú sokszögekre helyes, akkor n-szögekre is helyes.
Ezt a bizonyítást egy megjegyzéssel készítjük elő. Azt állítjuk, hogy ha egy sokszöget egymást nem metsző átlókkal háromszögekre bontunk fel, és a sokszög csúcsairól egynek kivételével tudjuk, hogy az páratlan sok háromszögnek a csúcsa, akkor ez minden csúcsra igaz. Ennek igazolása végett arra hivatkozunk, hogy minden átlónak két vége van, tehát az átlóvégek száma páros. Minthogy a kivételes csúcstól eltekintve minden csúcsról tudjuk, hogy páratlan sok háromszög ér oda, tehát ott páros sok (esetleg 0) átlóvég helyezkedik el, a kivételes csúcsra is páros sok átlóvég marad, s így az is páratlan sok háromszög csúcsa.
A teljes indukciós bizonyításra térve tekintsünk egy a feladat követelményét kielégítő módon felbontott, n>3 oldalú sokszöget, s ennek egy a felbontásában fellépő AB átlóját. Minthogy az A csúcsban ettől az átlótól eltekintve páratlan sok átló vége helyezkedik el, az AB átló egyik oldalán ezeknek az átlóvégeknek a száma páros. Ezen az oldalon az AB átló n-szögünkből egy S1 sokszöget vág le. Az n-szög felbontása S1-et is háromszögekre bontja fel. Erről a felbontásról megállapíthatjuk, hogy minden B-től különböző csúcsnál páros sok átlóvég helyezkedik el. Az előre bocsátott megjegyzés szerint tehát ez B-re is teljesül, azaz S1 felbontása eleget tesz a feladat követelményének.
Az AB átlóihoz az S1-gyel átellenes oldalon a felbontás egy ABC háromszöge támaszkodik (2. ábra).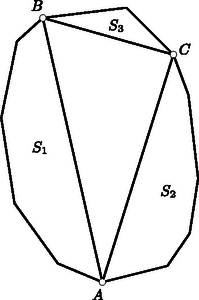
 
 

2. ábra
 

E háromszög AC, BC oldalai a háromszöggel átellenes oldalon n-szögünkből az S2 és S3 sokszöget vágják le. Az n-szöget eszerint az ABC háromszögre és az S1, S2, S3 sokszögekre bontottuk fel.
Minthogy az n-szöget felbontó átlók A-nál elhelyezkedő végei közül S1 belsejében páros sok van és kettő az ABC háromszög oldalának vége, S2 belsejében is páros sok helyezkedik el. Ugyanezt a B csúcsról és az S3-ban elhelyezkedő átlóvégekről is elmondhatjuk. Az előre bocsátott megjegyzés szerint tehát S2 és S3 felbontása is eleget tesz a feladat követelményének.
Mivel S1, S2 és S3 oldalszáma n-nél kisebb, indukciós feltevésünk szerint mindegyiknek az oldalszáma osztható 3-mal. Ezeknek az oldalszámoknak az összege azonban n+3, hiszen az ABC háromszög oldalai lépnek fel többletként. Így tehát n is osztható 3-mal.
 
III. megoldás. Először bebizonyítjuk, mégpedig teljes indukcióval, hogy egy sokszög egymást nem metsző átlókkal háromszögekre való felbontásakor a háromszögek két színnel kiszínezhetők úgy, hogy egyszínű háromszögeknek ne legyen közös oldala. Ez egyetlen háromszögre semmitmondóan igaz. Legyen tehát n>3, és tegyük fel, hogy az állítás n-nél kisebb oldalszámú sokszögekre igaz. Az egyik átló az n-szöget két sokszögre vágja fel. Minthogy ezek oldalszáma n-nél kisebb, indukciós feltevésünk szerint mindkettő a kívánt módon kiszínezhető a két színnel. Az egyikben a színeket esetleg felcserélve azt is elérhetjük, hogy a kettévágó átlóhoz a két sokszögben más-más színű háromszög támaszkodjék. Ilyen módon az n-szögnek a követelményünket kielégítő kiszínezéséhez jutottunk el.
Ha az n-szög felbontása eleget tesz feladatunk követelményének, akkor a háromszögek említett kiszínezésekor az n-szög oldalaihoz mindenütt ugyanolyan színű háromszög támaszkodik. Ezt elegendő két szomszédos oldalra belátnunk, s ezekre abból következik, hogy találkozási pontjukba páratlan sok háromszög ér el, s mivel ezek felváltva más-más színűek, a két szélső, tehát a sokszög említett két oldalára támaszkodó, ugyanolyan színű. A 3. ábra ilyen színezést mutat be.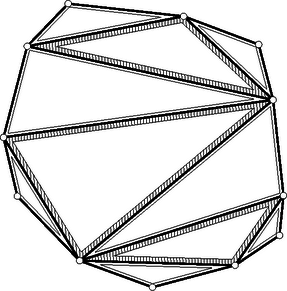
 

 

3. ábra
 

Az egyik színt a világos, a másikat a sötét keretezés szemlélteti. Ábránkban a sokszög határára mindenütt világos keretű háromszög támaszkodik.
Ha v világos és s sötét keretű háromszög szerepel, akkor ezeknek összesen 3v világosan és 3s sőtéten keretezett oldaluk van. Legyen a sokszög minden oldala világosan keretezett. Átlói két oldalról más-más keretet kaptak. Ezért a világosan keretezett oldalak számából a sötéten keretezettekét levonva a sokszög oldalszámát kapjuk meg:
n=3v-3s,
n tehát valóban 3-mal osztható.
 

Megjegyzések. 1. Második megoldásunk mintájára könnyű bebizonyítani a feladat állításának következő általánosítását: Egy konvex sokszöget egymást nem metsző átlók k-szögekre bontanak fel. A konvex sokszög minden csúcsa páratlan sok ilyen k-szög csúcsa. A sokszög oldalszáma ekkor
k[1+m(k-2)]
alakú, ahol m természetes szám. A bizonyítást az olvasóra hagyjuk.
2. Ugyancsak feladatként említjük meg Gallai Tibornak azt az eredményét, amely harmadik megoldásunk mintájára könnyen igazolható, s amely a következőképpen szól: Ha egy konvex sokszöget egymást nem metsző átlókkal háromszögekre bontunk fel, akkor az a páros sok csúcs, amelyben páros sok háromszög találkozik, a sokszög határvonalát töröttvonalakra bontja fel. Ha e töröttvonalak oldalszámait sorra váltakozó előjelekkel ellátva összeadjuk, 3-mal osztható eredményhez jutunk.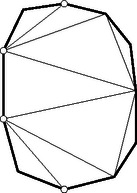
 
 

4. ábra
 

A 4. ábra sokszögénél a szóban forgó csúcsokat körökkel jelöltük meg. Ha a legalsó ilyen csúcstól pozitív forgásirányban haladunk, akkor váltakozó előjelekkel képzett összegként 6-2+1-2 adódik, ami valóban 3-mal osztható. Eredeti feladatunk a most közölt eredménynek azt a határesetét tartalmazza, amikor 0 azoknak a csúcsoknak a száma, ahol páros sok háromszög találkozik.