| Feladat: | 1965. évi Kürschák matematikaverseny 3. feladata | Korcsoport: 18- | Nehézségi fok: nehéz |
| Megoldó(k): | Gács Péter , Lovász László , Makai Endre , Pelikán József | ||
| Füzet: | 1966/május, 197 - 198. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Szabályos sokszög alapú gúlák, Négyszög alapú gúlák, Csonkagúlák, Tengely körüli forgatás, Szimmetrikus sokszögek, Trapézok, Négyszögek geometriája, Egyenlő szárú háromszögek geometriája, Derékszögű háromszögek geometriája, Geometriai egyenlőtlenségek, Középponti és kerületi szögek, Vetítések, Kürschák József (korábban Eötvös Loránd) | ||
| Hivatkozás(ok): | Feladatok: 1966/május: 1965. évi Kürschák matematikaverseny 3. feladata | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megoldás. Tekintsük az alapú, fedőlapú szabályos csonkgúlát (4. ábra). A forgásszimmetria miatt mindegy, hogy melyik testátló végpontjait összekötő vonalakkal foglalkozunk. Ha az testátlót választjuk, megállapíthatjuk, hogy minden összekötő vonalnak metszenie kell a térbeli hatszöget. Minthogy pedig e hatszög minden pontját -val és -vel a csonkagúla felületén elhelyezkedő szakasz köti össze, és két pont összekötő szakasza minden más összekötő vonalnál rövidebb, a legrövidebb összekötő vonal csak két szakaszból álló töröttvonal lehet. 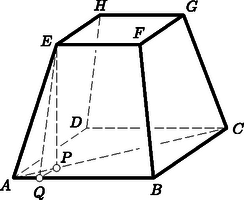 4. ábra Ez vagy egy oldallapon és a fedőlapon, vagy az alaplapon és egy oldallapon, vagy pedig két oldallapon helyezkedik el. A szimmetria miatt mindegy, hogy itt melyik oldallap vagy melyik két szomszédos oldallap szerepel. A vizsgált töröttvonal mindhárom esetben két olyan lapon halad, amelyek élben csatlakoznak. Ha e lapokat az él körül egy síkba forgatjuk, a töröttvonal is a síkba terül, s akkor lesz a legrövidebb, ha a kiterítés után nincs már törése, azaz a végpontokat összekötő egyetlen szakasszá válik. Ez persze csak akkor lehetséges, ha a kiterítés után adódó végpontok összekötő szakasza metszi a két lap közös élét. Megmutatjuk, hogy ez a bennünket érdeklő esetek mindegyikében bekövetkezik. Csonkagúlánk oldallapja szimmetrikus trapéz, melynek alapvonalán -nál nagyobb (és fedővonalán -nál kisebb) szögek nyugszanak. Ha ugyanis és az csúcsnak az alapsíkra, illetőleg az élre vetett vetülete, akkor az egyenlőszárú derékszögű, tehát miatt az -ben a nagyobbik befogóval szemközti . A feladat követelményére támaszkodva most azt igazoljuk, hogy . Az alaplap köré írt körben az húron -os (és -os) kerületi szögek nyugszanak. Minthogy az oldallap köré írt kör sugara nagyobb, ebben az húron nyugvó kerületi szögek -nál kisebbek és -nál nagyobbak. Mivel pedig az része a -nál kisebb -nek, valóban csak -nál kisebb lehet. Tekintsük most már az említett három esetnek megfelelő, kiterítéssel keletkező ábrákat (5. ábra). A testátló végpontjaiból a kiterítés után adódó pontokat összekötő (vastagon meghúzott) szakasz mind a három esetben metszi a két lap közös élét. Mindhárom esetben szerepel ugyanis olyan konvex négyszög, amelynek egyik átlója a közös él, másik átlója pedig a szóban forgó összekötő szakasz. E négyszögek két szemközti oldalát szaggatottan húztuk meg. Konvexitásuk csak az és ábrarészben kíván alátámasztást, s az ábrában , valamint , a ábrában pedig , valamint következménye. 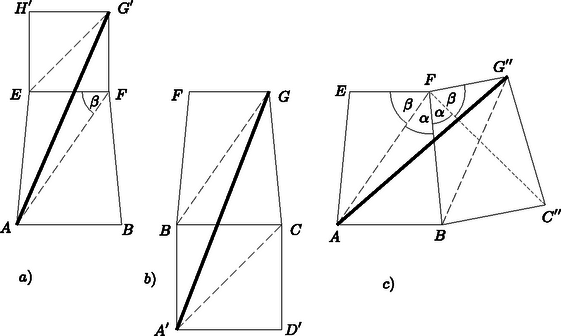 5. ábra Már csak annak megmutatására van szükségünk, hogy a vastagon meghúzott szakasz a ábrában a legrövidebb. A ábra szakasza nyilván hosszabb az ábráénál, hiszen vízszintes (a közös él egyenesére vetett) vetülete ugyanakkora, függőleges vetülete pedig nagyobb, mert az alapél nagyobb, mint a fedőél. Azt kell csak bizonyítanunk, hogy az és ábra szakaszaira . Ezek a szakaszok az és oldalai, amelyekben két-két oldal páronként egyenlő. Ezért az ismert tételre hivatkozva |