Feladat: 1965. évi Kürschák matematikaverseny 2. feladata Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Gács Péter ,  Laczkovich Miklós ,  Lovász László ,  Makai Endre ,  Pelikán József 
Füzet: 1966/május, 195 - 196. oldal  PDF  |  MathML 
Témakör(ök): Kör geometriája, Skatulyaelv, Geometriai egyenlőtlenségek, Háromszögek nevezetes tételei, Szabályos sokszögek geometriája, Rombuszok, Egyenlő szárú háromszögek geometriája, Thalesz-kör, Középponti és kerületi szögek, Pont körüli forgatás, Ponthalmazok, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1966/május: 1965. évi Kürschák matematikaverseny 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A 8 pont között legalább 7 a kör középpontjától különböző pont van. Minden ilyen pont a középponttal összekötve a kör egy-egy sugarát határozza meg. Ha ezek a sugarak nem mind különbözők, két pont ugyanannak a sugárnak a körközépponttól különböző pontja, s így távolságuk a sugárnál kisebb.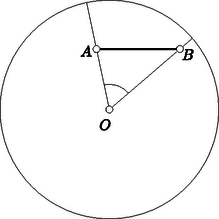
Ha viszont csupa különböző sugárhoz jutottunk, akkor ezek az O középpontnál elhelyezkedő teljes szöget legalább 7 szögre bontják fel, s ezért van közöttük két olyan sugár, amelynek szöge a teljes szög hatodrészénél, 60∘-nál kisebb. Legyen a 8 pont közül való A és B ezen a két sugáron (1. ábra).

 
 

1. ábra
 

Minthogy AOB∢<60∘, van az OAB▵-nek nagyobb szöge is. A háromszög szögeiről és szemközti oldalairól szóló tételre hivatkozva kimondhatjuk ezért, hogy az OAB▵-nek van AB-nél nagyobb oldala, hogy tehát AB kisebb az OA, OB távolságok valamelyikénél, s így kisebb az utóbbiaknál nem kisebb körsugárnál is.
Minden esetben eljutottunk tehát a 8 pont közül két olyanhoz, amely kielégíti a feladat követelményét.
 

II. megoldás. A körlemezt egy beírt szabályos hatszög csúcsaihoz vezető 6 sugár és ezek felezőpontjai által meghatározott szabályos hatszög segítségével 7 tartományra bontjuk fel (2. ábra). E tartományok mindegyike egy-egy olyan körben helyezkedik el, amelynek átmérője az eredeti kör sugara. Ez az eredeti körrel koncentrikus és feleakkora sugarú körre, valamint a beírt szabályos hatszög oldalaihoz tartozó Thales-körökre valóban teljesül.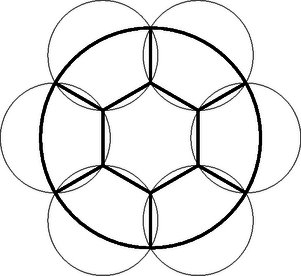
 

 

2. ábra

 

Tekintsük most a megadott 8 pontot és forgassuk el a kört tartományokra felosztó vonalakat a kör középpontja körül úgy, hogy a 8 pont egyike se essék felosztó vonalra. Ekkor a 7 tartomány valamelyikében legalább két pontnak kell elhelyezkednie. E két pont az illető tartományt leborító kör belsejében van, s így távolságuk a kör átmérőjénél, azaz az eredeti kör sugaránál kisebb.
 

Megjegyzések. 1) Nyilvánvaló, hogy a feladatban nem írhatunk 8 helyébe 7-et, hiszen a kör középpontja és egy beírt szabályos hatszög csúcsai 7 olyan pont, amelyek között nem lép fel a kör sugaránál kisebb távolság. Első megoldásunkból azt is kiolvashatjuk, hogy más ilyen ellenpélda nincs.
2) Jelölje an a körbe írt szabályos n-szög oldalát. A feladat állítása szerint a körlemezen felvett 8 pont között van kettő, amelynek távolsága a a6-nál kisebb. Bebizonyítjuk, hogy a két pont mindig megválasztható úgy is, hogy távolságuk ne legyen a7-nél nagyobb. A kör középpontja és egy beírt szabályos hétszög csúcsai mutatják, hogy a tétel állítása ilyen irányban tovább már nem finomítható.
A bizonyítás gondolatmenete második megoldásunkéhoz hasonló, de bizonyos szempontból azzal éppen ellentétes lesz. A kört most 8 tartományra bontjuk fel. Egy beírt szabályos hétszög leghosszabb átlói egy kisebb szabályos hétszöget burkolnak. Ennek csúcsai az eredeti hétszög csúcsaihoz vezető sugarakon helyezkednek el. A felbontást most a kisebb hétszög és a hétszögcsúcsokat összekötő sugárszakaszok szolgáltatják (3. ábra).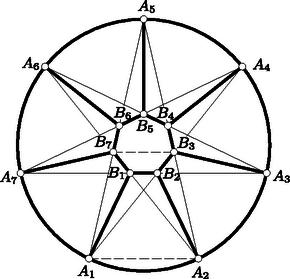
 
 

3. ábra
 

Azt állítjuk, hogy a 8 tartomány bármelyikén veszünk is fel két pontot (határpont felvételét is megengedve), ezek távolsága a7-nél nagyobb nem lehet. Ez a kis hétszög esetében nyilvánvaló, hiszen egy szabályos hétszög pontjai közül egy legnagyobb átló végpontjai vannak egymástól legtávolabbra, és a kis hétszög B7B3 átlója az ábra A1A2A5▵-éből kiolvashatóan kisebb, mint A1A2=a7.
A szektorszerű A1A2B2B1 tartományra térve először is belátjuk, hogy A1A2=A2B1 (s ugyanígy =A1B2). Ez abból adódik, hogy az A1A2B1A7 négyszög rombusz, mert szemközti oldalai párhuzamosak és A7A1=A1A2=a7, így tehát az A1B1 átló a rombuszból egyenlőszárú háromszöget vág le. Ennek szárszöge a kör egyharmadánál kisebb íven (ti. kéthetedén) nyugvó kerületi szög, ezért 60∘-nál kisebb, s így az egyenlőszárú háromszög A1B1 alapja az A1A2=a7 szárnál kisebb.
Ha a szektorszerű tartományban két egymástól maximális távolságra levő pontot keresünk, nyilván csak a határvonal pontjai jöhetnek szóba. A maximális szakasz végpontjai között nem szerepelhet egy határoló szakasz belső pontja, mert valamely pontnak egy szakasz pontjaitól mért távolságai közül a maximális értéket csak végponttól mért távolság adhatja. Nem szerepelhet a maximális szakasz végpontjai között az A1A2 körív belső pontja sem, mert a körlemez valamely (a középponttól különböző) pontjának egy körív pontjaitól mért távolságai közül a maximális értéket szintén csak végponttól mért távolság adhatja. Így tehát a keresett maximális szakasz mindkét végpontja csak az A1, A2, B2, B1 pontok közül való lehet, s e pontok távolságainak maximuma, mint láttuk, valóban a7.
Tekintsük most már a körlemez megadott 8 pontját. Ha mindannyian a kis hétszögben vannak, akkor bármelyik kettőnek a távolsága kisebb, mint a7. Ha nem ez a helyzet, forgassuk el a tartományainkat határoló vonalakat a kör középpontja körül úgy, hogy a 8 pont valamelyike elválasztó vonalra essék. Ekkor a tartományok mindegyike tartalmaz a belsejében és a határán valahány pontot (esetleg egyet sem) a 8 pont közül. E számok összege legalább 9 hiszen van olyan pont, amelyet kétszer is figyelembe vettünk. Kell tehát a 8 tartomány között olyannak lennie, amely a határát is hozzászámítva legalább két pontot tartalmaz pontjaink közül. E kettőnek a távolsága azonban a fentiek szerint legfeljebb a7, s ez állításunk helyességét bizonyítja.